Представление графической информации
Кривые на плоскости
Рассмотрим примеры построения кривых на плоскости.
Через две различные точки плоскости  и
и  , такие что
, такие что , можно провести прямую вида y = ax + b. Имеем:
, можно провести прямую вида y = ax + b. Имеем:
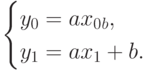
Если  , то эта система относительно a и b имеет единственное решение. Если
, то эта система относительно a и b имеет единственное решение. Если  , то уравнение прямой имеет вид:
, то уравнение прямой имеет вид:  . В общем виде прямая описывается уравнением
. В общем виде прямая описывается уравнением  .
.
В параметрическом виде отрезок, соединяющий точки 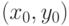 и
и 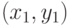 , определяется следующим образом:
, определяется следующим образом:
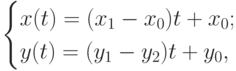
где  . Имеем:
. Имеем: 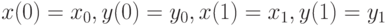 . В векторной форме данное соотношение записывается в виде:
. В векторной форме данное соотношение записывается в виде:
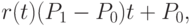
где
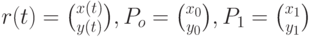
Аналогично, через три точки плоскости 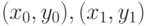 и
и 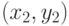 , абсциссы которых попарно различны, можно провести единственную кривую второго порядка, которая описывается многочленом второй степени (рис. 3.16 (a)). Его коэффициенты находятся из системы линейных уравнений относительно неизвестных a, b и c вида
, абсциссы которых попарно различны, можно провести единственную кривую второго порядка, которая описывается многочленом второй степени (рис. 3.16 (a)). Его коэффициенты находятся из системы линейных уравнений относительно неизвестных a, b и c вида
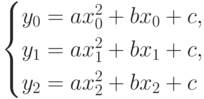
Определителем  данной системы является определитель Вандермонда порядка 3, так что
данной системы является определитель Вандермонда порядка 3, так что  .
.
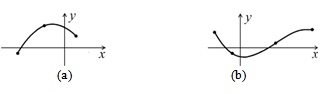
Рис. 3.16. (a) Парабола, проведенная через 3 точки; (b) кубическая парабола, проведенная через 4 точки
В общем случае, через n + 1 точку плоск n, который определяется однозначно, например, если абсциссы этих точек попарно различны. На рис. 3.16 (a) и (b) показаны примеры кривых, описываемых с помощью многочленов второй и третьей степени, которые проходят через 3 и через 4 заданные точки, соответственно.
Кривые на плоскости могут быть заданы
- явным образом с помощью одной или нескольких формул вида y = f(x), например
 ( рис. 3.17 (a));
( рис. 3.17 (a)); - неявно, с помощью неявной функции или функций вида F(x, y) = 0, например
 (рис. 3.17 (b));
(рис. 3.17 (b)); - параметрическим образом, например
 ,
, 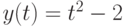 , где -
, где - 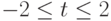 (рис. 3.17 (c)).
(рис. 3.17 (c)).
Кривые, приведенные на рис. 3.17 (a) и (c), являются кубическими, а кривая на рис. 3.17 (b) - квадратичной.
Обычно в компьютерной графике используются кубические сплайны, описываемые с помощью параметров. Кубическим сплайном называется гладкая функция, область определения которой разбита на конечное число отрезков, на каждом из которых эта функция совпадает с некоторым кубическим многочленом. При этом в концах отрезков совпадают не только значения этих многочленов, но и значения их первых и вторых производных.
Кривые Безье
Положим 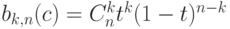 , где
, где  , k и n - целые,
, k и n - целые, 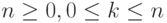 , а t принадлежит множеству действительных чисел.
, а t принадлежит множеству действительных чисел.
Полиномы 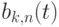 называются полиномами Берштейна.
называются полиномами Берштейна.
Пусть  - попарно различные точки плоскости, такие что
- попарно различные точки плоскости, такие что 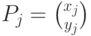 , для
, для  .
.
Кривой Безье называется параметрическая кривая степени n, которая определяется следующим образом:
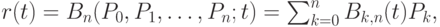
для  , где
, где  - координаты точек кривой Безье, соответствующих параметру t. Кривая названа по имени одного из ее изобретателей Пьера Безье (1962).
- координаты точек кривой Безье, соответствующих параметру t. Кривая названа по имени одного из ее изобретателей Пьера Безье (1962).
Заметим, что при t = 0 получается точка 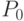 , а при t = 1 - точка
, а при t = 1 - точка 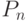 .
.
Если точка одна, то 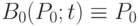 , так как
, так как 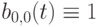 . Рассмотрим подробнее кривые Безье для n = 1, 2, 3.
. Рассмотрим подробнее кривые Безье для n = 1, 2, 3.
Пусть n = 1, и для построения кривой используются точки 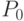 и
и 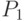 . Тогда кривая Безье описывается следующим образом:
. Тогда кривая Безье описывается следующим образом:
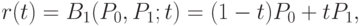
где ![t \in [0; 1]](/sites/default/files/tex_cache/73d01ee9450b0b5d3bb5cbb3e5e58ac2.png) . В матричной форме кривую можно представить в виде
. В матричной форме кривую можно представить в виде
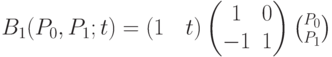
Координаты точек кривой удовлетворяют соотношению  (см. п. 3.2.2), так что кривая Безье представляет собой отрезок, соединяющий точки
(см. п. 3.2.2), так что кривая Безье представляет собой отрезок, соединяющий точки 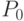 и
и 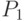 (рис. 3.18).
(рис. 3.18).
Пусть n = 2. Тогда кривая Безье описывается следующим образом: 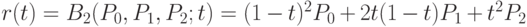 , где
, где ![t \in [0; 1]](/sites/default/files/tex_cache/73d01ee9450b0b5d3bb5cbb3e5e58ac2.png) , или, в матричной форме,
, или, в матричной форме,

Нетрудно заметить, что кривые Безье, построенные по трем точкам, являются квадратичными кривыми. Они используются, например, для создания шрифтов True Type.
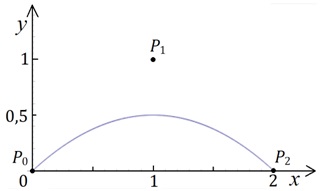
Пример 16. Найдем уравнение кривой Безье второго порядка, которая строится по точкам 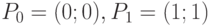 и
и 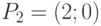 . Имеем:
. Имеем:
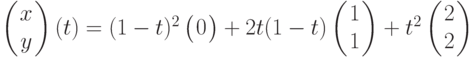
Поэтому 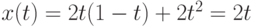 ; y(t) = 2t(1 - t), где
; y(t) = 2t(1 - t), где  . Следовательно, координаты x и y точек кривой Безье связаны соотношением:
. Следовательно, координаты x и y точек кривой Безье связаны соотношением:
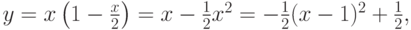
где 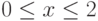 (рис. 3.19).
(рис. 3.19).
В компьютерной графике используются кубические кривые Безье, которые строятся по 4 точкам. Итак, пусть n = 3. Тогда кривая Безье задается формулой 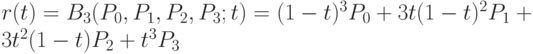 , где
, где ![t \in [0; 1]](/sites/default/files/tex_cache/73d01ee9450b0b5d3bb5cbb3e5e58ac2.png) . Соответственно, матричная форма имеет вид:
. Соответственно, матричная форма имеет вид: