Логические основы компьютера
Современные компьютеры являются многоуровневыми. Под уровнем понимается абстракция - гипотетическая виртуальная машина, которая имеет свое устройство, свой набор команд, который она может выполнять, и свой язык, на котором эти команды пишутся. Каждая такая абстракция надстраивается над абстракцией более низкого уровня. Более высокий уровень подразумевает команды более удобные для человека. Программа, написанная на языке уровня N, либо транслируется в программу на языке уровня N - 1, которая затем исполняется машиной, либо интерпретируется некоторой программой уровня N - 1, которая последовательно исполняет команды программ уровня N.
Нижним (ниже нулевого) является уровень физических устройств, на котором находятся транзисторы. Нулевым называют цифровой логический уровень - аппаратное обеспечение компьютера. Над ним последовательно располагаются уровень микроархитектуры, уровень архитектуры набора команд, уровень операционной системы, уровень ассемблера и уровень языка прикладных программистов.
В основе аппаратного обеспечения лежат вентили - миниатюрные электронные устройства, которые моделируются в виде цифровых устройств, входы и выходы которых принимают значения 0 и 1 - цифровые сигналы. Значение 0 соответствует низкому напряжению, а значение 1 - высокому. При конструировании электронных устройств используются законы алгебры логики, или булевой алгебры высказываний, поэтому эти устройства называют логическими.
Настоящая лекция посвящена булевой алгебре высказываний, логическим элементам и схемам логических функций, которые применяются при конструировании цифровых компьютеров, а также битовым операциям, которые лежат в основе обработки цифровых сигналов и которые используются в языках программирования высокого уровня.
Логические функции
Основу любого дискретного вычислительного устройства составляют электронные логические схемы, работа которых базируется на законах алгебры логики.
Понятие высказывания
Высказывание - первичное, неопределяемое понятие, как множество или информация. Под высказыванием понимают четко сформулированное утверждение о каких-либо фактах, о котором можно определенно сказать, истинно оно или ложно. Оно не может быть одновременно истинным и ложным.
Пример 1. Следующие утверждения являются высказываниями:
- "После пятницы наступает суббота";
- "Входное напряжение низкое";
- "2 + 2 = 5".
Простыми называют высказывания, никакие части которых высказываниям не являются. Из простых высказываний с помощью логических связок, которым соответствуют связки естественного языка, конструируются сложные высказывания. Простые высказывания связок не содержат.
Пример 2. Рассмотрим простые высказывания A и B:
A: "В классе идут занятия"; B: "За окном светит солнце".
Примером сложного высказывания является
A и не B: "В классе идут занятия, а за окном солнце не светит".
Высказывания могут принимать значения истина или ложь, которые называют истинностными значениями. Им соответствуют значения 1 и 0, соответственно, которые в дальнейшем также будут использоваться в качестве истинностных значений.
Операции над высказываниями
Рассмотрим основные операции над высказываниями. Пусть S - множество высказываний. Операцией арности n называется отображение
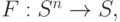
где n - целое неотрицательное число. Арностью называется число аргументов. При n = 1 операция называется унарной, при n = 2 - бинарной, при n = 3 - тернарной.
Примером унарной операции является отрицание. Отрицанием высказывания A называется высказывание  , которое истинно в точности тогда, когда A ложно.
, которое истинно в точности тогда, когда A ложно.
Пример 3. Для высказывания A: "Идет дождь", отрицанием является высказывание 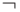 A: "Не идет дождь".
A: "Не идет дождь".
Отрицанием высказывания B: "Высокое напряжение", является высказывание 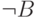 : "Низкое напряжение", если напряжение может быть только низким или высоким.
: "Низкое напряжение", если напряжение может быть только низким или высоким.
Ниже приведены определения бинарных операций.
Конъюнкцией высказываний A и B называется высказывание A & B, которое истинно ровно тогда, когда истинны оба высказывания A и B.
Дизъюнкцией высказываний A и B называется высказывание 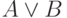 , которое истинно в точности тогда, когда истинно хотя бы одно из высказываний A и B.
, которое истинно в точности тогда, когда истинно хотя бы одно из высказываний A и B.
Импликацией высказываний A и B называется высказывание 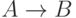 , которое ложно в точности тогда, когда A истинно, а B ложно.
, которое ложно в точности тогда, когда A истинно, а B ложно.
Эквиваленцией высказываний A и B называется высказывание  , которое истинно в точности тогда, когда высказывания A и B имеют одно и то же истинностное значение.
, которое истинно в точности тогда, когда высказывания A и B имеют одно и то же истинностное значение.
Строгой, или разделительной дизъюнкцией высказываний A и B называется высказывание  , которое истинно в точности тогда, когда ровно одно из высказываний A и B является истинным.
, которое истинно в точности тогда, когда ровно одно из высказываний A и B является истинным.
Штрихом Шеффера высказываний A и B называется высказывание  , которое ложно в точности тогда, когда оба высказывания A и B истинны.
, которое ложно в точности тогда, когда оба высказывания A и B истинны.
Стрелкой Пирса высказываний A и B называется высказывание  , которое истинно в точности тогда, когда оба высказывания A и B ложны.
, которое истинно в точности тогда, когда оба высказывания A и B ложны.
Пример 4. Возьмем высказывания A: "Аня пойдет в кино" и B: "Боря пойдет в кино". Имеем:
 "Аня и Боря оба пойдут в кино";
"Аня и Боря оба пойдут в кино";
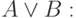 "Хотя бы один из Ани и Бори пойдет в кино";
"Хотя бы один из Ани и Бори пойдет в кино";
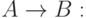 "Если Аня пойдет в кино, то и Боря пойдет в кино";
"Если Аня пойдет в кино, то и Боря пойдет в кино";
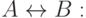 "Аня и Боря либо оба пойдут в кино, либо оба не пойдут";
"Аня и Боря либо оба пойдут в кино, либо оба не пойдут";
 "Кто-то из Ани и Бори пойдет в кино, но не оба";
"Кто-то из Ани и Бори пойдет в кино, но не оба";
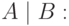 "Хотя бы один из Ани и Бори не пойдет в кино";
"Хотя бы один из Ани и Бори не пойдет в кино";
 "Аня и Боря оба не пойдут в кино".
"Аня и Боря оба не пойдут в кино".
Рассмотрим формальное определение языка логики высказываний, в который в качестве логических связок добавлены символы, обозначающие строгую дизъюнкцию, штрих Шеффера и стрелку Пирса, так как они играют важную роль в цифровых схемах.
Язык логики высказываний
Формальный язык задается:
- алфавитом, содержащим символы языка;
- синтаксисом, определяющим, как из символов строятся формулы;
- семантикой - интерпретацией элементов языка с помощью приписывания значений символам алфавита.
Алфавит языка логики высказываний состоит из символов:
- пропозициональные символы, или переменные:
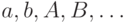 ;
; - логические связки:
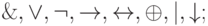
- вспомогательные символы: запятая и скобки.
Понятие высказывания, или пропозициональной формулы (формулы логики высказываний) определяется индуктивно:
- пропозициональные символы являются высказываниями, или атомарными формулами (или атомами);
- если A и B - высказывания (формулы), то
 - высказывания (формулы).
- высказывания (формулы). - других высказываний, кроме построенных с помощью первых двух правил, не существует.
Конечные последовательности символов языка называют выражениями. Правильно построенные выражения (высказывания) строятся по приведенным выше правилам. Например, выражение 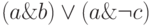 является высказыванием, а выражение
является высказыванием, а выражение 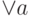 не является.
не является.
Рассмотрим семантику языка логики высказываний.
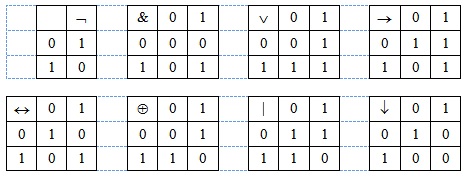
На множестве {0, 1} определим логические операции, которые обозначим так же, как и операции на множестве высказываний, через 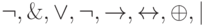 и
и 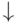 . Определение этих операций приведено в рис. 4.1.
. Определение этих операций приведено в рис. 4.1.
Пусть - множество высказываний.
Истинностным означиванием называется функция  , для которой выполняются свойства:
, для которой выполняются свойства:
-
 ;
; -
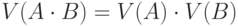 , где символ
, где символ  обозначает один из символов
обозначает один из символов 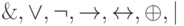 или
или  .
.