Логические основы компьютера
Пример 13. Секретные документы находятся в одном из трех сейфов. Три агента передали по два сообщения - одно о том, в каком сейфе находятся документы, и одно о том, в каком сейфе их нет.
Первый агент:
- "Документы не в первом сейфе";
- "Документы во втором сейфе".
Второй агент:
- "Документы не в первом сейфе";
- "Документы в третьем сейфе".
Третий агент:
- "Документы не в третьем сейфе";
- "Документы в первом сейфе".
Стало известно, что оба сообщения одного из агентов верны, оба сообщения другого агента неверны, а еще один агент прислал одно верное сообщение, а другое неверное. Требуется определить, в каком сейфе находятся секретные документы.
Введем высказывания:
a: "Документы в первом сейфе";
b: "Документы во втором сейфе";
с: "Документы в третьем сейфе".
Tогда сообщения агентов могут быть представлены в виде:
первый агент: 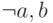 ;
;
второй агент: 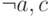 ;
;
Имеем:  , так как документы находятся только в одном сейфе. Возможны три случая.
, так как документы находятся только в одном сейфе. Возможны три случая.
-
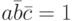 , или a = 1, b = 0, c = 0. В этом случае оба сообщения первых двух агентов неверны, что, по условию, невозможно.
, или a = 1, b = 0, c = 0. В этом случае оба сообщения первых двух агентов неверны, что, по условию, невозможно. -
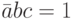 , или a = 0, b = 1, c = 0. Тогда второй и третий агенты прислали по одному верному сообщению и по одному неверному, что противоречит условию задачи.
, или a = 0, b = 1, c = 0. Тогда второй и третий агенты прислали по одному верному сообщению и по одному неверному, что противоречит условию задачи. -
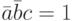 , или a = 0, b = 0, c = 1. В этом случае первый агент прислал одно верное сообщение и одно неверное, второй - два верных, третий - два неверных, так что все условия выполняются.
, или a = 0, b = 0, c = 1. В этом случае первый агент прислал одно верное сообщение и одно неверное, второй - два верных, третий - два неверных, так что все условия выполняются.
Таким образом, секретные документы находятся в третьем сейфе.
Понятие логической функции
Пусть B = {0, 1} и n - натуральное число.
Логическая, или булевская функция - это функция вида
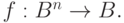
Если логическая функция имеет n аргументов, то область ее определения содержит  элементов, а всего таких функций
элементов, а всего таких функций 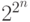
Пример 14. Пусть n = 1. Все логические функции с одним аргументом имеют вид:
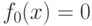 для
для 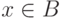 ;
;
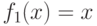 для
для 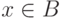 ;
;
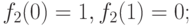
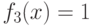 для
для 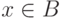 .
.
Логические функции имеют конечное число аргументов, поэтому такие функции могут определяться в виде таблиц истинности. В табл. 4.3 определены функции из примера 14.
Переменная, которая принимает значения на множествеB, называется булевской, или логической.
Высказывание можно рассматривать как логическую функцию, в которой пропозициональные переменные соответствуют булевским, а операции определены так, как показано в рис. 4.1.
Пример 15. Функция  вида
вида 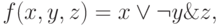 для
для  , является логической функцией.
, является логической функцией.
Пример 16. Всего имеется 16 логических функций с 2 аргументами, восемь из них определены в табл. 4.1. В табл. 4.4 приведено определение оставшихся восьми функций с помощью формул логики высказываний.
| A | B | 0 | 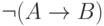 |
A | 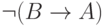 |
B |
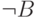 |
 |
1 |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 |
| 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 1 |
| 1 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 1 |
Покажем, что любая логическая функция может быть представлена с помощью операций конъюнкции, дизъюнкции и отрицания.
Утверждение 3. Пусть 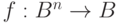 - логическая функция. Тогда
- логическая функция. Тогда
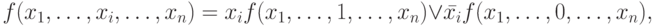
для  ;
;
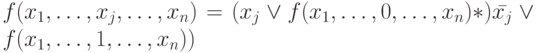
для 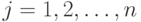 .
.
Доказательство. Если 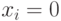 , то обе части первого равенства совпадают с
, то обе части первого равенства совпадают с 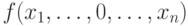 , а если
, а если 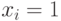 , то с
, то с  , для
, для  . Аналогично, если
. Аналогично, если  , то обе части второго равенства совпадают с
, то обе части второго равенства совпадают с 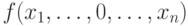 , а если
, а если 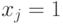 , то с
, то с  , для
, для 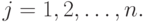
И утверждения 3 следует следующее утверждение.
Утверждение 4. Пусть 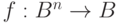 - логическая функция. Тогда
- логическая функция. Тогда
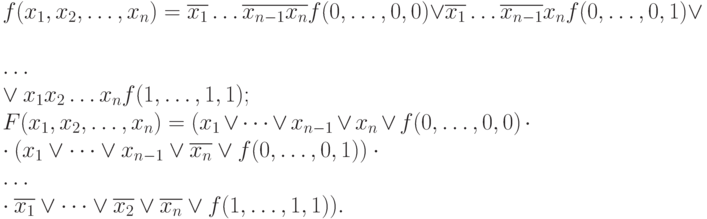
Доказательство. Обе формулы нетрудно проверить с помощью индукции по числу аргументов.
Элементарной конъюнкцией (дизъюнкцией) называется конъюнкция (дизъюнкция) булевских переменных или их отрицаний, в которую каждая переменная входит не более одного раза. Равными называются элементарные конъюнкции (дизъюнкции), отличающиеся только порядком следования переменных или их отрицаний.
Дизъюнктивной (конъюнктивной) нормальной формой называется дизъюнкция (конъюнкция) неповторяющихся элементарных конъюнкций (дизъюнкций). Сокращенно она обозначается ДНФ (КНФ). Если в каждую элементарную конъюнкцию (дизъюнкцию) входит каждая переменная, то эта форма называется совершенной дизъюнктивной (конъюнктивной нормальной формой и сокращенно обозначается СДНФ (СКНФ).
Из утверждения 4 следует, что представление логической функции в СДНФ единственно, с точностью до порядка следований элементарных конъюнкций. Аналогично для СКНФ.
Если в таблице истинности значение функции для набора аргументов равно 0, то в СКНФ присутствует дизъюнкция этого набора переменных и отрицаний переменных, указанная в утверждении 4, а в СДНФ отсутствует, соответственно, конъюнкция отрицаний этого набора переменных и отрицаний переменных, и наоборот.
Пример 17. Найдем СДНФ функции 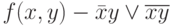 и определим, при каких значениях аргументов она принимает значение 1. Имеем:
и определим, при каких значениях аргументов она принимает значение 1. Имеем:
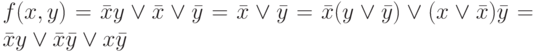
Из утверждения 4 следует, что

Поэтому f(0,0)=f(0,1)=f(1,0) , а f(1,1)=0 .
Пример 18. Найдем СДНФ и СКНФ логической функции, которая соответствует таблице истинности 4.5.
| x | y | z | f |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
СДНФ функции выглядит следующим образом:

Она упрощается до ДНФ: 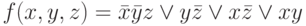 .
.
СКНФ функции имеет вид:

Определим операции на множестве логических функций из 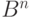 в B.
в B.
Пусть 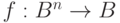 и
и 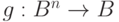 . Положим
. Положим
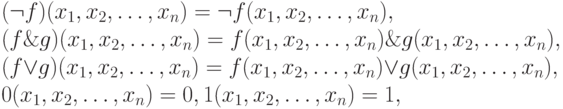
для  .
.
Утверждение 5. Множество логических функций из Bn в B с определенными выше операциями образуют булеву алгебру.
Доказательство. Нетрудно проверить, что так определенные операции удовлетворяют всем свойствам 1 - 5 из п. 4.1.4.