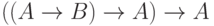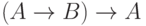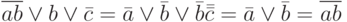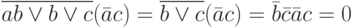Логические основы компьютера
Пример 5. Пусть a и b - высказывания, V(a) = 0, V(b) = 1. Тогда
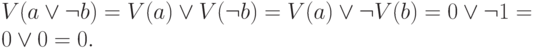
В общем случае, означивание атомарных высказываний однозначно определяет означивание формулы (это можно доказать с помощью индукции по числу логических связок, которые содержит формула).
Все способы означивания пропозициональной формулы перечисляются с помощью таблиц истинности. В табл. 4.1 приведены таблицы истинности для операций, определенных выше.
 |
 |
 |
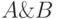 |
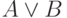 |
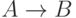 |
 |
 |
 |
 |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 |
Формула, которая всегда истинна, т. е. истинна для любых означиваний переменных, называется тавтологией.
Невыполнимой формулой, или противоречием, называется всегда ложная формула.
Пример 6. Высказывание  является тавтологией, а высказывание
является тавтологией, а высказывание 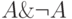 - противоречием.
- противоречием.
Проверим с помощью таблицы истинности, что высказывание 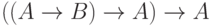 является тавтологией ( табл. 4.2).
является тавтологией ( табл. 4.2).
В записи формул соблюдаются следующие приоритеты относительно символов логических связок: сначала 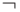 , потом
, потом 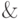 и
и 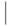 , после этого
, после этого 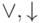 и
и  , затем
, затем 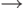 и, наконец,
и, наконец, 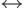 . Порядок применения операций с одинаковым приоритетом регулируется скобками.
. Порядок применения операций с одинаковым приоритетом регулируется скобками.
Пример 7. Следующие высказывания являются тавтологиями:
-
 ;
; -
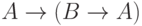 ;
; -
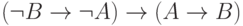 ;
; -
 .
.
Свойства логических операций
Две формулы называются равными, или эквивалентными, если их значения совпадают для любых означиваний переменных. Обозначим через 1 тавтологию, а через 0 - противоречие.
Ниже перечислены основные свойства логических операций:
- a & b = b & a;
-
 ;
; -
ассоциативность операций
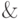 и
и 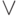 :
: (a & b) & с = a & (b & с);
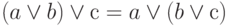 ;
; -
законы поглощения:
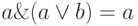 ;
;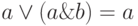 ;
; -
дистрибутивность:
 ;
; -
дополнительность (законы 0 и 1):
 ;
; ,
,
для произвольных элементов a, b и c (все свойства легко проверить с помощью таблиц истинности).
Замечание 1. Множество операций конъюнкции, дизъюнкции и отрицания обладает свойством полноты: остальные логические операции можно выразить через эти три. В самом деле,
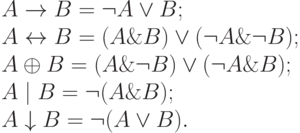
Таким образом, для произвольного высказывания существует эквивалентное ему высказывание, содержащее из связок только 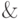 ,
, 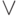 и
и 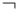 .
.
Замечание 2. Множество операций конъюнкции и отрицания обладает свойством полноты. Действительно, 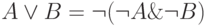 .
.
Замечание 3. Множество операций дизъюнкции и отрицания обладает свойством полноты. В самом деле, 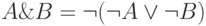 .
.
Замечание 4. Штрих Шеффера обладает свойством полноты. Действительно, 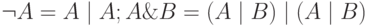 .
.
Замечание 5. Стрелка Пирса обладает свойством полноты. В самом деле, 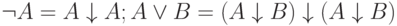 .
.
Свойства операций используются для упрощения формул.
В дальнейшем знак 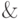 иногда заменяется знаком * или опускается, а отрицание формулы a обозначается в виде
иногда заменяется знаком * или опускается, а отрицание формулы a обозначается в виде  .
.
Пример 8. Имеем:
Понятие булевой алгебры
Множество M, на котором определены бинарные операции 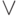 и
и 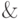 и унарная операция
и унарная операция 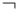 , для которых выполняются свойства 1 - 4 из п. 4.1.4 (коммутативность, ассоциативность, дистрибутивность и законы поглощения), и в котором существуют элементы 0 и 1, удовлетворяющие свойству 5 (законы 0 и 1), называется булевой алгеброй.
, для которых выполняются свойства 1 - 4 из п. 4.1.4 (коммутативность, ассоциативность, дистрибутивность и законы поглощения), и в котором существуют элементы 0 и 1, удовлетворяющие свойству 5 (законы 0 и 1), называется булевой алгеброй.
Символы 0 и 1 обозначают некоторые элементы множества M, а символы 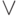 ,
, 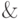 и
и 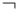 - операции на этом множестве. Операция
- операции на этом множестве. Операция 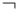 называется операцией дополнения, или отрицания. Операции
называется операцией дополнения, или отрицания. Операции 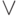 и
и 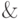 по-прежнему будут называться операциями дизъюнкции и конъюнкции, соответственно.
по-прежнему будут называться операциями дизъюнкции и конъюнкции, соответственно.
Равенства, выражающие свойства 1 - 5 булевой алгебры, перечисленные в п. 4.1.4, называются еще тождествами булевой алгебры.
Пример 9. Множество {0, 1} c операциями дизъюнкции, конъюнкции и отрицания является булевой алгеброй.
Пример 10. Множество высказываний S c операциями дизъюнкции, конъюнкции и отрицания является булевой алгеброй.
Пример 11 (булева алгебра множеств). Пусть M - множество. Множество подмножеств M c операциями объединения, пересечения и дополнения до M является булевой алгеброй. Здесь 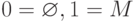 .
.
Утверждение 1. Булева алгебра обладает следующим свойством:
если a & b = a & c и  , то b = c.
, то b = c.
Доказательство. Имеем:
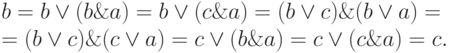
Замечание. Если в каждом равенстве из свойств 1 - 5 одновременно заменить символ 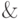 на символ
на символ  , символ
, символ  на символ
на символ 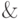 , а также 0 на 1 и 1 на 0, то множество равенств не изменится. Символы
, а также 0 на 1 и 1 на 0, то множество равенств не изменится. Символы 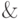 и
и  , а также символы 0 и 1 называются двойственными.
, а также символы 0 и 1 называются двойственными.
Равенства, полученные заменой символов на двойственные им, называются двойственными. Если из тождеств булевой алгебры следует какое-либо равенство, то следует и двойственное ему равенство.
Утверждение 2. Операции булевой алгебры обладают следующими свойствами:
-
конъюнкция с 1 и дизъюнкция с 0:
a & 1 = a;
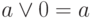 ;
; -
идемпотентность операций
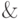 и
и  :
:a & a = a;
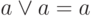 ;
; -
конъюнкция с 0 и дизъюнкция с 1:
a & 0 = 0;
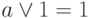 ;
; -
дополнение 0 и 1:
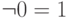 ;
; -
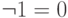 ;
; -
инволютивность дополнения:
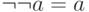 ;
; -
законы де Моргана:
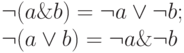
для произвольного элемента a множества M.
Доказательство. Докажем по одному из двойственных равенств, второе равенство получается взаимной заменой двойственных символов:
-
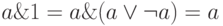 (по закону 0 и 1 и закону поглощения);
(по закону 0 и 1 и закону поглощения); -
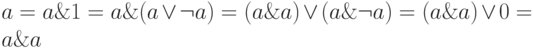 (по закону 0 и 1 и закону дистрибутивности);
(по закону 0 и 1 и закону дистрибутивности); -
 ,
, -
 ;
; -
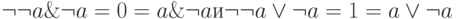 ,
,следовательно, по утверждению 1,
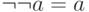 ;
; -
аналогично,
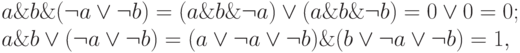
поэтому
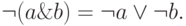
Следствие 1. Элементы 0 и 1 в булевой алгебре единственны. В самом деле, пусть имеются элементы 0' и 1' из множества M, такие что 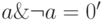 и
и  для произвольного элемента a из M. Тогда
для произвольного элемента a из M. Тогда
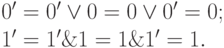
Следствие 2. 1) Если a & b = 1, то a = 1 и b = 1.
2) Если 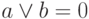 , то a = 0 и b = 0.
, то a = 0 и b = 0.
Действительно, пусть  . Тогда
. Тогда
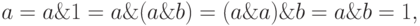
и, точно так же, b = 1. Аналогично для двойственного утверждения.
Логические задачи
Рассмотрим примеры решения логических задач с помощью алгебры логики.
Пример 12. Аня, Боря, Витя, Гриша и Даша решают, пойти ли им в кино. Ситуация описывается следующими высказываниями:
- Если Аня пойдет, то и Боря пойдет;
- Хотя бы кто-то из Вити и Гриши пойдет;
- В кино пойдет либо Боря, либо Даша, но не оба;
- Витя и Даша либо оба пойдут в кино, либо оба не пойдут;
- Если Гриша пойдет, то пойдут также Аня и Витя.
Предполагая, что все высказывания истинны, определите, кто пойдет в кино.
Введем атомарные высказывания:
a: "Аня пойдет в кино"; b: "Боря пойдет в кино";
v: "Витя пойдет в кино";g: "Гриша пойдет в кино";
d: "Даша пойдет в кино".
Представим в виде высказываний условия задачи:
-
 ;
; -
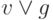 ;
; -
 ;
; -
 ;
; -
 .
.
Выразим все операции через операции конъюнкции, дизъюнкции и отрицания. В результате получим:
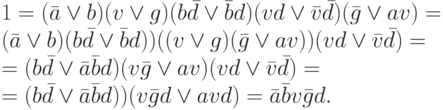
Поэтому  следовательно, a=0, b=0, v=0, g=0, d=0,
следовательно, a=0, b=0, v=0, g=0, d=0,
так что, Витя и Даша пойдут в кино, а Аня, Боря и Гриша не пойдут.