Игры. Клеточные автоматы
Настоящая лекция посвящена конечным детерминированным играм и клеточным автоматам.
Дискретная детерминированная игра двух лиц с полной информацией - это игра, в которой существует конечное множество позиций, в ней участвуют два игрока, которые ходят по очереди, и каждый ход игрока приводит к новой позиции, при этом игрок владеет всей информацией о позиции, в которой ему предстоит сделать ход, и обо всех допустимых ходах в этой позиции. Правила игры определяют начальную позицию игры, допустимые ходы игрока в каждой позиции, какая позиция является конечной, а также кто выигрывает, и при каких условиях объявляется ничья. Последовательность ходов и соответствующих им позиций, которая приводит от начальной позиции к конечной позиции, называется партией игры.
Конечные автоматы описывают состояния конечного множества элементов в дискретные моменты времени. Клеточные автоматы определяются пятью составляющими: множеством клеток, правилом определения соседних клеток, множеством состояний, начальным состоянием клеток и правилом перехода из текущего состояния в следующее состояние - из одного момента времени в следующий момент.
Рассматривается игра "Ним". Для поиска выигрышных ходов применяются битовые операции. Доказываются теоремы Бутона и Шпрага-Гранди. Приводятся примеры применения функции Шпрага-Гранди для поиска выигрышных стратегий в играх, представимых в виде суммы более простых игр. Кроме этого, обсуждаются элементарные клеточные автоматы, игра "Жизнь" - двумерный клеточный автомат и ее варианты.
Игра "Ним". Теорема Шпрага-Гранди
Игра называется справедливой, если игроки в ней равноправны.
Математическая игра - это справедливая дискретная детерминированная игра двух лиц с полной информацией, в которой через конечное число шагов достигается либо выигрышная позиция для одного из игроков, либо ничейная, если она возможна. Игрок называется правильным, если он всегда ходит наилучшим образом. Игра с правильными игроками называется правильной игрой.
Ниже рассматриваются только математические игры.
Позиция для игрока называется выигрышной, если при правильной игре она приводит этого игрока к выигрышу. Позиция называется проигрышной, если при правильной игре она приводит к проигрышу. Ход для игрока называется выигрышным, если он приводит к проигрышной для противника позиции, и проигрышным, если противник получает выигрышную позицию. Таким образом, выигрышной является позиция, в которой игрок может сделать такой ход, что как бы ни играл его противник, его позиции всегда будут выигрышными. Соответственно, проигрышной является такая позиция игрока, что любой его ход приведет к позиции, выигрышной для противника. Стратегией игры является алгоритм выбора правильного хода. Стратегия называется выигрышной, если она приводит игрока к выигрышу.
Рассмотрим игру "Ним" - математическую игру, в которой все позиции делятся на выигрышные и проигрышные, поэтому она всегда заканчивается выигрышем одного игрока и проигрышем другого.
Игра "Ним" заключается в следующем. Имеется n кучек камней (или других однородных предметов). Два игрока ходят по очереди. За один ход разрешается взять любое ненулевое число камней из одной кучки. Выигрывает тот, кто берет последний камень ( рис. 5.1).
Позицию в игре "Ним" можно описать в виде набора целых неотрицательных чисел 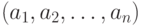 , которые равны числу камней в кучках. Если
, которые равны числу камней в кучках. Если  , то позиция называется нулевой.
, то позиция называется нулевой.
Игра "Ним" с двумя кучками
Найдем выигрышную стратегию для игры "Ним".
Пусть кучка одна. Тогда первый игрок забирает сразу все камни и выигрывает. Таким образом, в случае одной кучки начальная позиция является выигрышной для первого игрока.
Для упрощения перебора будем описывать позицию 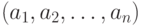 так, чтобы выполнялось соотношение
так, чтобы выполнялось соотношение 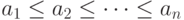 . Кроме того, на множестве позиций игры с n кучками введем отношение линейного порядка, аналогичного лексикографическому порядку для слов
. Кроме того, на множестве позиций игры с n кучками введем отношение линейного порядка, аналогичного лексикографическому порядку для слов 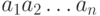 .
.
Пусть кучек две. Позиция (0, k) является выигрышной для любого натурального k. Позиция (1, 1) - проигрышная. Любая позиция вида (1, k), где k > 1, является выигрышной, так как за один ход ее можно свести к проигрышной позиции. Наименьшей позицией, которая не сводится к проигрышной позиции (1, 1) за один ход, является позиция (2, 2). Позиция (2, 2) также является проигрышной, так как любой ход из нее приводит к выигрышной позиции. Соответственно, позиции вида (2, k), для k > 2, являются выигрышными. Следующей проигрышной позицией является (3, 3). Рассуждая аналогичным образом, получим, что проигрышная позиция в игре с двумя кучками содержит одинаковое число камней в кучках. Следовательно, выигрышная стратегия в игре с двумя кучками - выравнивать число камней в кучках.
Таким образом, если в начальной позиции обе кучки содержат равное число камней, то она является проигрышной для первого игрока, а если неравное, то выигрышной.
Игра "Ним" с тремя кучками
Пусть имеется три кучки. Из предыдущих рассуждений следует, что для m > 0 позиции (0, 0, m) являются выигрышными, а позиции (0, m, m) - проигрышными. Соответственно, позиции вида (k, m, m), для  , и (m, m, k), для k > m, являются выигрышными.
, и (m, m, k), для k > m, являются выигрышными.
Наименьшей позицией, которая не сводится за один шаг к найденным проигрышным позициям, является (1, 2, 3). Поэтому данная позиция является проигрышной. Нетрудно видеть, что позиции (1, 4, 5) и (1, 6, 7) также являются проигрышными.
Наименьшей позицией, которая начинается с 2 и не сводится за один шаг к найденным проигрышным позициям, является позиция (2, 4, 6), затем идет (2, 5, 7).
Пример 1. Рассмотрим игру "Ним" с тремя кучками, содержащими 3, 5 и 7 камней ( рис. 5.1).
Все проигрышные позиции для этой игры имеют вид:
(0, k, k), для k от 1 до 5 включительно;
(1, 2, 3), (1, 4, 5), (2, 4, 6), (2, 5, 7), (3, 4, 7), (3, 5, 6).
Поэтому в позиции (3, 5, 7) существует 3 выигрышных хода: если игрок возьмет 1 камень из первой, второй или третьей кучки, то получится позиция (2, 5, 7), (3, 4, 7) или (3, 5, 6), соответственно. Все эти позиции являются проигрышными для второго игрока. Таким образом, позиция (3, 5, 7) является выигрышной для первого игрока. Выигрышная стратегия первого игрока - ходить так, чтобы противник получал проигрышную позицию.
Общее описание проигрышных позиций для игры "Ним" с тремя кучками приводится ниже. Если число кучек больше трех, то с помощью перебора можно найти проигрышные позиции аналогичным образом.
Рассмотрим более простой способ поиска выигрышной стратегии в игре Ним.
Свойства побитовой операции строгой дизъюнкции
Утверждение 1. Побитовая операция  обладает следующими свойствами:
обладает следующими свойствами:
-
 ;
; -
 ;
; -
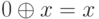 ;
; -
 ,
,
для произвольных целых неотрицательных чисел x, y и z.
Доказательство. Очевидно, что свойства выполняются на множестве {0, 1}. Поэтому они выполняются и для каждого двоичного разряда в двоичном представлении чисел x, y и z..
Утверждение 2. Побитовая операция  на множестве неотрицательных целых чисел обладает следующими свойствами:
на множестве неотрицательных целых чисел обладает следующими свойствами:
-
 тогда и только тогда, когда x = y;
тогда и только тогда, когда x = y; - Если
 , то y = z.
, то y = z.
Доказательство. 1) Пусть  . Тогда
. Тогда  .
.
Если x = y, то 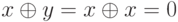
2) Пусть  . Тогда
. Тогда 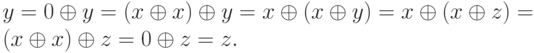
Игра "Ним" известна в течение нескольких столетий, но первым ее полное решение опубликовал Чарльз Бутон в 1901 г. В теореме Бутона описываются проигрышные позиции этой игры, а также ее выигрышная стратегия.

