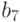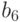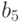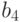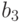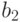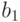Игры. Клеточные автоматы

Игра "Жизнь". Понятие клеточного автомата

Рассмотрим примеры клеточных автоматов, которые имеют широкое применение в различных областях исследований.

Клеточный автомат - это пятерка 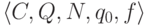, где

• C - множество клеток;
• Q - множество состояний клетки;
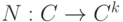• - правило определения окрестности клетки;
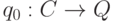• - начальное состояние клеток;
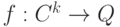• - правило перехода из состояния в состояние.

Окрестность клетки образуют соседние с ней клетки (или ее соседи), а также сама клетка. Начальным является состояние множества клеток в момент времени 0. Правило перехода определяет, каким будет состояние клетки в момент времени i + 1, в зависимости от того, каким было ее состояние, а также состояние ее соседей в момент времени i.

Ниже рассматриваются примеры клеточных автоматов, в которых клетки могут принимать одно из двух состояний: 0 или 1.

Элементарные клеточные автоматы

Элементарный клеточный автомат - это одномерный автомат в виде бесконечной ленты, в котором соседними для клетки являются клетки, содержащие с ней общую сторону. Таким образом, каждая клетка имеет два соседа. Правило изменения состояния клетки определяется логической функцией с тремя аргументами, которыми являются состояния клеток ее окрестности. Всего существует 256 элементарных клеточных автоматов, по числу логических функций с 3 аргументами.

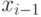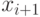Пусть - клетка, а и - ее соседи слева и справа, соответственно. Пусть также N - целое число, такое что 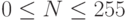, и двоичное представление числа N длины 8 имеет вид: . Правило Вольфрама, или правило N, описывает переходы между состояниями в элементарном клеточном автомате, в соответствии с таблицей истинности логической функции, которая представлена в табл. 5.1.

Если клетка в момент времени k находится в состоянии 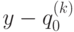, а ее соседи в состояниях 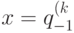и 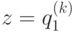, соответственно, то состояние клетки xi в момент k + 1 имеет вид: .

Таблица 5.1. Правило N

x	y	z	f
0	0	0
0	0	1
0	1	0
0	1	1
1	0	0
1	0	1
1	1	0
1	1	1

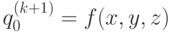Пример 8. Рассмотрим правило 110. Имеем:

Преобразование состояния клетки по правилу 110 имеет вид:

000	001	010	011	100	101	110	111
 0	 1	 1	 1	 0	 1	 1	 0

(ср. с таблицей истинности).

Множество состояний элементарного клеточного автомата представляется в виде конечного клеточного поля, строки которого соответствуют моментам времени. Обычно правая сторона поля отождествляется с левой, так что правым соседом крайней правой клетки является крайняя левая клетка, а левым соседом крайней левой клетки - крайняя правая клетка. Например, пусть поле имеет 9 клеток, начальное состояние центральной клетки равно 1, а остальных клеток - 0. Тогда по правилу 110 состояния клеточного поля в моменты времени 1 - 4 имеют вид:

Состояние множества клеток одномерного поля в момент времени k отображается в виде k-го ряда двумерного поля. Белый цвет клетки обозначает состояние 0, а черный - состояние 1. Например, если в начальный момент времени состояние 1 имеет только крайняя правая клетка, то последующие 29 состояний одномерного поля для правила 110 выглядят так, как показано на рис. 5.6 (a), где начальное состояние соответствует нижнему ряду поля.

Пример 9. Для числа 18 имеем: 18 = 000100102.

Поэтому правило 18 можно представить следующим образом:

На рис. 5.6 (b) правило 18 применяется к одномерному множеству клеток, образующему нижний ряд поля, в начальном состоянии которого 10 клеток, выбранных случайным образом, имеют состояние 1, а остальные клетки - состояние 0. Как и ранее, левая и правая границы поля отождествляются.

Рис. 5.6. Клеточные автоматы для правила (a) 110; (b) 18; начальное состояние соответствует нижнему ряду поля

Игра "Жизнь"

Игру "Жизнь" придумал в 1970 г. американский математик Джон Конвей. Она является клеточным автоматом, множество клеток которого представляет собой бесконечное двумерное клеточное поле. Соседними считаются клетки, имеющие хотя бы одну общую вершину, поэтому каждая клетка имеет 8 соседей. Клетки могут находиться в одном двух состояний - 0 или 1. В первом случае клетка называется пустой, или мертвой, а в втором - живой.

Правила Конвея размножения и гибели клеток имеют вид:

• если пустая клетка имеет ровно 3 живых соседа, то в ней зарождается жизнь - она становится живой;
• если живая клетка имеет 2 или 3 живых соседа, то она сохраняет жизнь - остается живой;
• если клетка имеет менее 2 или более 3 живых соседей, то она становится пустой - умирает от недостатка или перенасыщения, соответственно.

Игра прекращается, если на поле не остается ни одной живой клетки или конфигурация живых клеток станет неизменяемой, или устойчивой.

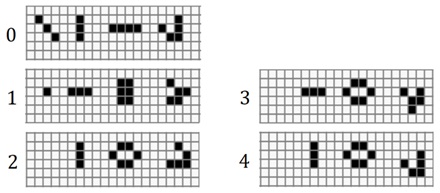
Пример 10. На рис. 5.7 приведен фрагмент игры для четырех фигур в момент времени k, для k от 0 до 4. Крайняя левая фигура ("диагональ") погибает на втором шаге. Вторая фигура, справа от нее, называется "мигалка" - это периодически повторяющаяся конфигурация с периодом 2. Третья фигура на втором шаге переходит в устойчивое состояние ("улей"). Четвертая фигура ("планер") за каждые четыре шага смещается по диагонали на одну клетку в направлении вправо-вниз.

Рис. 5.7. Состояния конфигурации живых клеток в моменты времени от 0 до 4

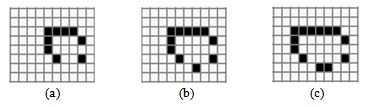
Пример 11. Рассмотрим конфигурации живых клеток, которые называются "космическими кораблями". Каждая такая конфигурация перемещается - начальное взаимное расположение живых клеток периодически повторяется, при этом фигура смещается на 2 клетки по направлению движения: передней частью "корабля" является отрезок, содержащий в начальном состоянии 3 клетки. "Легкий", "средний" и "тяжелый космические корабли" показаны на рис. 5.8 (a-c).

Рис. 5.8. Космический корабль: (a) легкий; (b) средний; (c) тяжелый

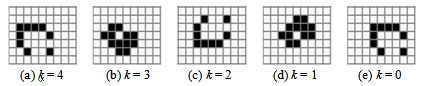
На рис. 5.10 (a-e) показано перемещение "легкого корабля".

Рис. 5.10. Легкий космический корабль в моменты времени k от 0 до 4

Пример 12. Примером повторяющей без смещения конфигурации живых клеток с периодом 3 является кембриджский пульсар ( рис. 5.11).

Рис. 5.11. Кембриджский пульсар в момент времени (a) 0; (b) 1; (с) 2

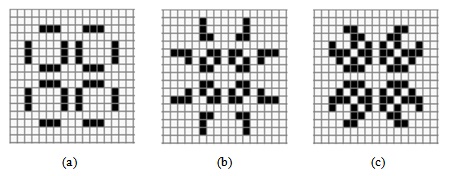
На рис. 5.12 (a-c) приведены примеры конфигураций живых клеток, каждая из которых за конечное время преобразуется в кембриджский пульсар.

Рис. 5.12. Конфигурации, сходящиеся к кембриджскому пульсару

Периодически повторяющиеся фигуры называют осцилляторами.

Начальные конфигурации живых клеток, которые стабилизируются через большое число поколений, называются фигурами Мафусаила, по имени библейского персонажа, который дольше всех из допотопных жителей. Примеры таких конфигураций приведены на рис. 5.12 (a-c).

Рис. 5.12. Фигуры Мафусаила: (a) "пентамино"; (b) "желудь"; (c) "кролики"

Фигуры "пентамино", "желудь" и "кролики" стабилизируются соответственно через 1103, 5206 и 17332 поколений.