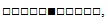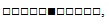Игры. Клеточные автоматы
Варианты игры "Жизнь"
Появление игры "Жизнь" привело к созданию клеточных автоматов со схожей структурой. Их называют жизнеподобными (Life-like) клеточными автоматами. Правила "зарождения" и "сохранения" жизни обозначаются в виде  , где
, где 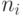 - число живых соседей, при которых пустая клетка становится живой, а
- число живых соседей, при которых пустая клетка становится живой, а 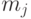 - число живых соседей, при которых живая клетка остается живой, где
- число живых соседей, при которых живая клетка остается живой, где 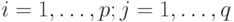 . Для оригинальной игры "Жизнь" правило имеет вид: B3/S23.
. Для оригинальной игры "Жизнь" правило имеет вид: B3/S23.
Примерами известных жизнеподобных автоматов являются:
- "Высшая жизнь" (High Life): B36/S23;
- "Репликатор" (Replicator): B1357/S1357;
- "Лабиринт" (Maze): B3/S12345;
- "Фредкин" (Fredkin): B1357/S02468;
- "День и ночь" (Day & Night): B3678/S34678.
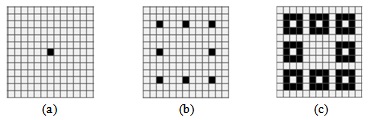
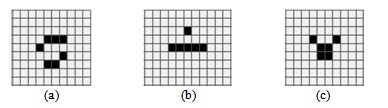
На рис. 5.13 (a-c) показаны некоторые состояния клеточного автомата "Репликатор", в котором каждая конфигурация является репликатором - бесконечно копирует себя.
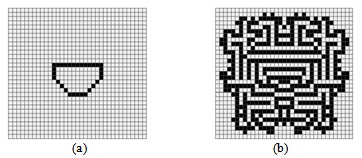
Клеточный автомат "Лабиринт" создает изображения, похожие на лабиринт, из любого начального состояния ( рис. 5.14 (a-b) ).
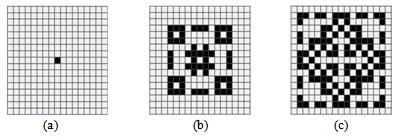
Клеточный автомат "Фредкин" порождает расширяющиеся конфигурации ( рис. 5.15 (a-c)).
У клеточного автомата "День и ночь" на бесконечном поле существуют периодические конфигурации живых клеток, которые при замене мертвых клеток живыми, а живых - мертвыми преобразуются в конфигурации, которые так же являются пери
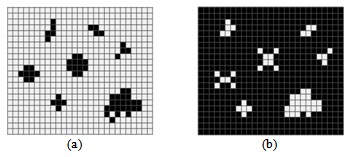
Рис. 5.16. "День и ночь": периодические конфигурации (a) живых клеток; (b) пустых клеток на поле из живых клеток
Игра "Жизнь" на гексагональном поле
Для создания жизнеподобных клеточных автоматов, помимо прямоугольного поля, используется гексагональное поле, в котором клетки являются правильными шестиугольниками. На бесконечном поле каждая клетка обладает шестью соседями.
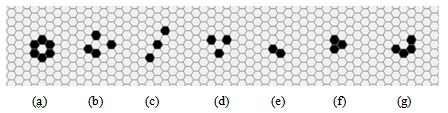
На рис. 5.17 (a-g) показаны примеры осцилляторов для жизнеподобного клеточного автомата, правило "зарождения" и "сохранения" жизни которого имеет вид: B2/S34.
Упражнение. Найдите период каждого осциллятора, приведенного на рис. 5.17.
На гексагональном поле существуют также стохастические клеточные автоматы, в которых пустая клетка становится живой с некоторой вероятностью, при заданном количестве соседей.
Например, пустая клетка становится живой с вероятностью  , если она имеет ровно 2 живых соседа; живая клетка остается живой, если у нее имеется 1 или 2 живых соседа. Другим примером является клеточный автомат, в котором пустая клетка оживает с вероятностью 1, если имеет 3 живых соседа, и с вероятностью
, если она имеет ровно 2 живых соседа; живая клетка остается живой, если у нее имеется 1 или 2 живых соседа. Другим примером является клеточный автомат, в котором пустая клетка оживает с вероятностью 1, если имеет 3 живых соседа, и с вероятностью  , если она имеет 2 живых соседа; живая клетка сохраняет жизнь, если она имеет 2 или 3 живых соседа.
, если она имеет 2 живых соседа; живая клетка сохраняет жизнь, если она имеет 2 или 3 живых соседа.
Упражнения
- Пусть x - неотрицательное целое число. Покажите, что если x четное, то
 , а если нечетное, то
, а если нечетное, то  .
. -
Найдите выигрышный ход в игре "Ним", если он существует, в позиции
a) (19, 15, 4);
b) (8, 4, 12, 22);
c) (14, 25, 17, 3, 10).
-
Перечислите все проигрышные позиции в игре "Ним" с тремя кучками, если число камней в каждой кучке не превосходит
a) 10;
b) 15;
c) 20.
-
Постройте функцию Шпрага-Гранди и придумайте выигрышную стратегию для игры в камни с одной кучкой. В игре участвуют два игрока, игроки ходят по очереди. Выигрывает игрок, который берет последний камень. Кучка содержит m камней. За один ход игрок может взять от 1 до k камней, если k равно
4;
b) 7.
- Придумайте выигрышную стратегию для игры в камни с n кучками. В игре участвуют два игрока, игроки ходят по очереди. За один ход игрок может взять от 1 до 7 камней из любой кучки. Выигрывает игрок, который берет последний камень. Постройте функцию Шпрага-Гранди для этой игры.
- Придумайте выигрышную стратегию для "мизерного" варианта игры "Ним", который отличается от исходной игры только тем, что игрок, берущий последний камень, проигрывает, а не выигрывает.
-
Рассмотрим игру в N. В игре участвуют два игрока, Игроки ходят по очереди. Имеется пять костяшек домино с очками от 1 до 5. Первый игрок кладет монету на любую костяшку и получает число очков, обозначенное на этой костяшке. Второй игрок перекладывает монету на любую другую костяшку и получает число очков, равное сумме очков другого игрока и очков, обозначенных на этой костяшке. Оставлять монету на той же костяшке нельзя, и так далее. Выигрывает игрок, который набирает ровно N очков или принуждает противника превзойти эту сумму. Придумайте выигрышную стратегию для игры в N, если она существует, для значения N, равного
a) 2;
b) 6;
с) 7;
d) 13;
e) 21;
f) 37.
-
Опишите с помощью клеток правила перехода для элементарного клеточного автомата, соответствующего правилу
a) 24;
b) 135;
с) 215.
-
Постройте логическую функцию, которая соответствует переходам в элементарном клеточном автомате для правила
a) 110;
b) 30;
с) 150.
-
Найдите состояния 1 - 10 элементарного клеточного автомата с начальным состоянием
,если для переходов используется правило
a) 110;
b) 18;
c) 218;
d) 150;
e) 53;
f) 30.
-
Найдите состояния 1 - 10 элементарного клеточного автомата с начальным состоянием
1)
;2)
,в котором правило перехода определяется логической функцией
a)
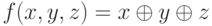 ;
;b)
 .
. -
Найдите состояния 1 - 10 элементарного клеточного автомата с начальным состоянием
1)
;2)
,в котором правило определяется алгебраической функцией
a) f(x, y, z) = (x + y + z) mod 2,;
b) f(x, y, z) = (x y + x z) mod 2.
-
Определите, через сколько шагов становится устойчивой или периодической конфигурация живых клеток в игре "Жизнь", приведенная на рис. 5.18:
-
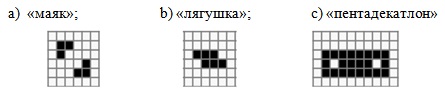
Определите период приведенной на рис. 5.19 конфигурации живых клеток в игре "Жизнь":
a) "маяк";
b) "лягушка";
c) "пентадекатлон"
-
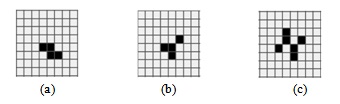
Определите для жизнеподобной игры с правилом B3/S3, период осциллятора, приведенного на рис. 5.20:
-
Определите для жизнеподобной игры с правилом B3/S13, период осциллятора, приведенного на рис. 5.18: