Сбалансированные деревья

Скошенные деревья бинарного поиска

В методе вставки в корень, описанном в "Таблицы символов и деревья бинарного поиска" , перемещение вновь вставленного узла в корень дерева выполнялось с помощью левой и правой ротации. В этом разделе исследуются способы модификации метода вставки в корень, чтобы ротации еще и в определенном смысле балансировали дерево.

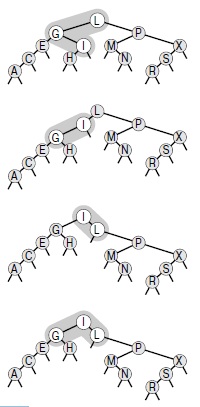
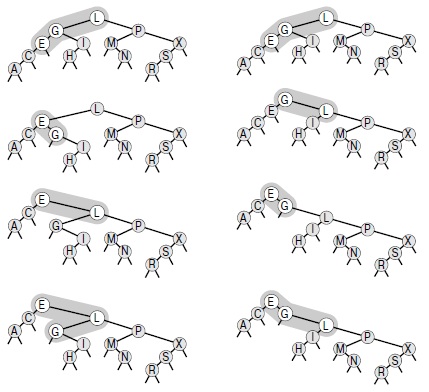
Вместо того чтобы рассматривать (рекурсивно) единственную ротацию, которая перемещает последний вставленный узел в вершину дерева, рассмотрим две ротации, которые перемещают узел из позиции в одном из узлов-внуков корня в вершину дерева. Вначале выполняется одна ротация, перемещающая узел в дочернюю позицию корня. Затем при помощи еще одной ротации он перемещается в корень. Здесь возможны два принципиально различных случая, в зависимости от того, одинаково ли ориентированы две ссылки от корня к вставляемому узлу. На рис. 13.5 показан случай, когда ориентации различны, а на рис. 13.6 изображен случай с одинаковыми ориентациями. В основе обработки скошенных BST-деревьев лежит наблюдение о существовании другого способа выполнения действий, когда ссылки от корня к вставляемому узлу ориентированы одинаково: достаточно выполнить две ротации в корне, как показано в правой части рис. 13.6.

Скошенная вставка (splay insertion) перемещает вновь вставленные узлы в корень, применяя трансформации, показанные на рис. 13.5 (стандартная вставка в корень, если ссылки от корня к узлу-внуку на пути поиска имеют различную ориентацию) и в правой части рис. 13.6 (две ротации в корне, если ссылки от корня к узлу-внуку на пути поиска имеют одинаковую ориентацию). Построенные таким образом BST-деревья называются скошенными BST-деревьями (splay BST). Программа 13.5 является рекурсивной реализацией скошенной вставки; пример одиночной вставки приведен на рис. 13.7, а пример построения дерева показан на рис. 13.8. Различие между скошенной и стандартной вставками в корень может показаться несущественным, но оно достаточно важно: операция скоса исключает худший случай квадратичного времени выполнения — главный недостаток стандартных BST-деревьев.

Рис. 13.5. Двойная ротация в BST-дереве (ориентации различны)

В приведенном дереве (вверху) в результате ротации влево в узле G, за которой следует ротация вправо в узле L, узел I помещается в корень (внизу). Эти ротации могут завершать процесс вставки в стандартном или скошенном BST-дереве.

Константа, подразумеваемая в O-нотации, равна 3. Например, для построения BST-дерева из 100 000 узлов с помощью скошенных вставок всегда требуется менее 5 миллионов сравнений. Это не гарантирует, что полученное дерево поиска будет хорошо сбалансировано или что каждая операция будет эффективной, но очень важна полученная гарантия общего времени выполнения; на практике фактическое время выполнения, скорее всего, окажется еще меньше.

При скошенной вставке узла в BST-дерево выполняется не только перемещение этого узла в корень, но и перемещение всех встретившихся на пути поиска узлов ближе к корню. Точнее говоря, выполняемые ротации уменьшают расстояние от корня до любого встретившегося узла в два раза. Это свойство сохраняется также и при такой реализации операции найти, когда операции скоса выполняются во время поиска.

Некоторые пути в деревьях удлиняются; если обращение к узлам на этих путях не выполняется, то это не имеет значения. Если же мы обращаемся к узлам на длинном пути, то после этого он укорачивается вдвое; поэтому ни один путь не сопряжен с большими затратами.

Рис. 13.6. Двойная ротация в BST-дереве (ориентации одинаковы)

Когда обе ссылки в двойной ротации ориентированы в одном направлении, существуют две возможности. В стандартном методе вставки в корень вначале выполняется ротация в узле, расположенном ниже (слева); а при скошенной вставке вначале выполняется вставка в узле, расположенном выше (справа).

Лемма 13.5 представляет собой гарантию амортизированной производительности: это эффективность не каждой операции, а средних затрат всех выполненных операций. Это среднее значение не является вероятностным; скорее утверждается, что общие затраты будут гарантированно низкими. Для многих приложений такой гарантии достаточно, но для некоторых других приложений этого может оказаться мало. Например, при использовании скошенных BST-деревьев нельзя гарантировать время ответа для каждой операции, поскольку время выполнения некоторых операций может быть линейным. Если какая-либо операция выполняется за линейное время, то тогда другие операции будут выполняться гораздо быстрее, но это слабое утешение для вынужденного ожидать клиента.

Граничное значение, приведенное в свойстве 13.5 — это граница общих затрат на все операции в худшем случае. Как это обычно бывает для граничных значений в худшем случае, они могут быть гораздо выше фактических затрат. Операция скоса перемещает последние посещенные элементы ближе к вершине дерева; поэтому данный метод удобен для приложений поиска с неравномерной структурой запросов — особенно для приложений со сравнительно небольшим, или даже медленно изменяющимся, набором элементов, к которым выполняется обращение.

Программа 13.5. Скошенная вставка в BST-дерево

Эта функция отличается от алгоритма вставки в корень из программы 12.13 лишь одной существенной особенностью: если путь поиска из корня проходит влево-влево или вправо-вправо, узел перемещается в корень путем двойной ротации от вершины, а не от нижней части (см. рис. 13.6).

Программа проверяет четыре варианта для двух шагов пути поиска от корня и выполняет соответствующие ротации:

• влево-влево: дважды выполняет ротацию влево в корне;
• влево-вправо: выполняет ротацию влево в левом дочернем узле, а затем вправо в корне;
• вправо-вправо: дважды выполняет ротацию вправо в корне;
• вправо-влево: выполняет ротацию вправо в правом дочернем узле, а затем влево в корне.

  private:
    void splay(link& h, Item x)
      { if (h == 0)
          { h = new node(x, 0, 0, 1); return; }
        if (x.key() < h->item.key())
          { link& hl = h->l; int N = h->N;
            if (hl == 0)
              { h = new node(x, 0, h, N+1); return; }
            if (x.key() < hl->item.key())
              { splay(hl->l, x); rotR(h); }
            else
              { splay(hl->r, x); rotL(hl); }
            rotR(h);
          }
        else
          { link &hr = h->r; int N = h->N;
            if (hr == 0)
              { h = new node(x, h, 0, N+1); return; }
            if (hr->item.key() < x.key())
              { splay(hr->r, x); rotL(h); }
            else
              { splay(hr->l, x); rotR(hr); }
            rotL(h);
          }
        }
    public:
      void insert(Item item)
        { splay(head, item); }
      

На рис. 13.9 приведены два примера, демонстрирующие эффективность операций скоса-ротации для балансировки дерева. На этих рисунках вырожденное дерево (построенное вставками элементов в порядке их ключей) приводится в сравнительно хорошо сбалансированное состояние с помощью небольшого числа операций найти.

Обобщая, можно сказать, что небольшое количество выполненных поисков существенно улучшает сбалансированность дерева.

Рис. 13.7. Скошенная вставка

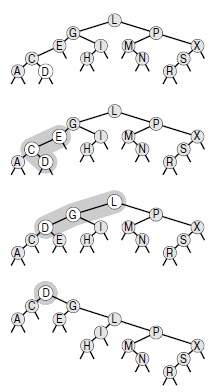
На этом рисунке изображен результат (внизу) вставки записи с ключом D в дерево, приведенное на верхнем рисунке, с помощью скошенной вставки в корень. В данном случае процесс вставки состоит из двойной ротации влево-вправо, за которой следует двойная ротация вправо-вправо (от вершины).

Рис. 13.8. Построение скошенного дерева

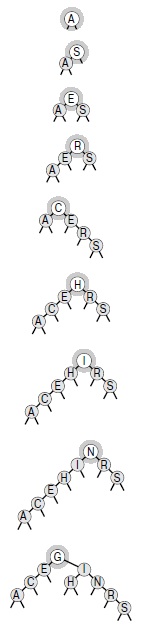
Здесь показана последовательность скошенных вставок записей с ключами A S E R C H I N G в первоначально пустое дерево.

Рис. 13.9. Балансировка худшего случая скошенного дерева с помощью серии поисков

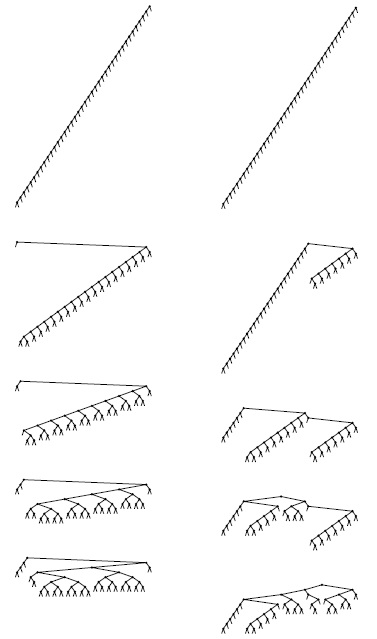
Скошенная ставка упорядоченных ключей в первоначально пустое дерево требует только постоянного количества шагов для выполнения одной вставки, но создает несбалансированное дерево, показанное вверху слева и справа. Левая последовательность рисунков показывает результат поиска (со скосом) самого наименьшего, второго, третьего и четвертого наименьших ключей в дереве. Каждый поиск вдвое уменьшает длину пути к искомому ключу (и к большинству других ключей в дереве).

Правая последовательность рисунков показывает балансировку этого же худшего случая дерева серией случайных успешных поисков. Каждый поиск уменьшает вдвое количество узлов в своем пути, заодно уменьшая длину путей поиска и множества других узлов в дереве. Небольшое количество поисков существенно улучшает сбалансированность дерева.

Если в дереве могут быть повторяющиеся ключи, то операция скоса может привести к тому, что элементы с ключами, равными ключу в данном узле, попадут по обе стороны от этого узла (см. упражнение 13.38). Из этого следует, что найти все элементы с данным ключом будет не так легко, как в случае стандартных BST-деревьев. Необходимо либо проверять наличие равных ключей в обоих поддеревьях, либо воспользоваться каким-либо альтернативным методом обработки повторяющихся ключей из описанных в "Таблицы символов и деревья бинарного поиска" .

Упражнения

13.25. Нарисуйте скошенное BST-дерево, образованное скошенными вставками элементов с ключами E A S Y Q U T I O N в указанном порядке в первоначально пустое дерево.

13.26. Сколько ссылок дерева должно быть изменено для выполнения двойной ротации? Сколько ссылок действительно изменяется при выполнении каждой из двойных ротаций в программе 13.5?

13.27. Добавьте в программу 13.5 реализацию операции найти со скосом.

13.28. Реализуйте нерекурсивную версию функции скошенной вставки из программы 13.5.

13.29. Используйте программу-драйвер из упражнения 12.30 для определения эффективности скошенных BST-деревьев как самоорганизующихся структур поиска, сравнив их со стандартными BST-деревьями для распределения поисковых запросов, определенных в упражнениях 12.31 и 12.32.

13.30. Нарисуйте все структурно различные BST-деревья, которые могут быть получены скошенными вставками N ключей в первоначально пустое дерево, для 2 < N < 7.

13.31. Определите вероятность того, что каждое из деревьев в упражнении 13.30 образовано вставками N случайных различных элементов в первоначально пустое BST-дерево.

13.32. Определите эмпирически среднее значение и среднеквадратичное отклонение количества сравнений, используемых при успешном и неудачном поиске в BST-дереве, построенном скошенными вставками N случайных ключей в первоначально пустое дерево, при N = 10³, 10⁴, 10⁵ и 10⁶ . Не следует выполнять сами операции поиска: просто постройте деревья и вычислите длину их путей. Являются ли скошенные BST-деревья более сбалансированными, чем произвольные BST-деревья, или менее, или одинаково?

13.33. Добавьте в программу из упражнения 13.32 выполнение N случайных (скорее всего, неудачных) поисков со скосом в каждом из созданных деревьев. Как влияет скос на среднее количество сравнений при неудачном поиске?

13.34. Добавьте в программы из упражнений 13.32 и 13.33 возможность измерения времени их выполнения вместо подсчета количества сравнений. Проведите те же эксперименты. Объясните любые изменения в выводах, получаемых из экспериментальных результатов.

13.35. Сравните применение скошенных BST-деревьев со стандартными BST-деревьями в задаче построения индекса по фрагменту реального текста, содержащего по меньшей мере 1 миллион символов. Измерьте время, требуемое для построения индекса и средние длины путей в BST-деревьях.

13.36. Определите экспериментально среднее количество сравнений при успешном поиске в скошенном BST-дереве, построенном вставками произвольных ключей, при N = 10³, 10⁴, 10⁵ и 10⁶ .

13.37. Проверьте экспериментально идею использования скошенных вставок, а не стандартных вставок в корень, для рандомизированных BST-деревьев.

13.38. Нарисуйте скошенное BST-дерево, образованное вставками элементов с ключами 0 0 0 0 0 0 0 0 0 0 0 0 1 в указанном порядке в первоначально пустое дерево.