Очереди с приоритетами и пирамидальная сортировка

Очереди с приоритетами для индексных элементов

Предположим, что записи, обрабатываемые в очереди с приоритетами, находятся в некотором массиве. В этом случае программам обработки очередей с приоритетами имеет смысл обращаться к элементам по индексам массива. Более того, использование индексов массива в качестве дескрипторов позволяет реализовать все операции, выполняемые над очередями с приоритетами. Интерфейс, соответствующий этому описанию, приведен в программе 9.11. На рис. 9.13 показан небольшой пример применения такого подхода. Можно получить очередь с приоритетами, содержащую некоторое подмножество записей, и обойтись без копирования и специальных изменений в записях. Использование индексов существующего массива — вполне естественное решение, однако оно ведет к реализациям с ориентацией, противоположной программе 9.8.

Программа 9.11. Интерфейс АТД очереди с приоритетами для индексных элементов

Вместо построения различных структур данных из самих элементов данных, этот интерфейс позволяет построить очередь с приоритетами, используя индексы элементов клиентского массива. Подпрограммы, реализующие операции вставить, извлечь наибольший, изменить приоритет и извлечь, используют дескрипторы в виде индексов массива, а клиентская программа перегружает операцию < так, чтобы стало возможным сравнение двух элементов массива. Например, клиентская программа может определить операцию < таким образом, что значением неравенства i < j становится результат сравнения data[i].grade и data[j].grade.

  template <class Item>
  class PQ
    { private:
        // Программный код, зависящий
        // от реализации
      public:
        PQ(int);
        int empty() const;
        void insert(Index);
        Index getmax();
        void change(Index);
        void remove(Index);
    };
        

Рис. 9.13. Структуры данных индексного пирамидального дерева

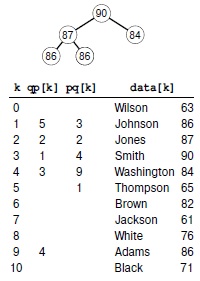
Работа не с записями, а с индексами этих записей позволяет создать очередь с приоритетами из подмножества записей, хранящихся в массиве. В этом примере пирамидальное дерево размера 5 в массиве pq содержит индексы студентов с пятью наивысшими оценками. То есть data[pq[1]].name содержит фамилию студента с наивысшей оценкой — Smith и т.д. Обратный массив qp позволяет подпрограммам обработки очередей с приоритетами работать с индексами массива как с дескрипторами. Например, если понадобится изменить оценку Смита на 85, нужно будет изменить значение data[3].grade, а затем вызвать PQchange(3). Реализация очереди с приоритетами обращается к записи как pq[qp[3]] (то есть pq[1], поскольку qp[3]=1,), а к новому ключу как data[pq[1]].name (то есть data[3].name, поскольку pq[1]=3).

Теперь уже клиентская программа не может свободно перемещать информацию, поскольку программа обработки очереди с приоритетами работает с индексами для данных, используемых клиентом. А реализация очереди с приоритетами должна пользоваться индексами только после получения их от клиента.

При разработке реализации применяется в точности такой же подход, что и для индексной сортировки в разделе 6.8 "Элементарные методы сортировки" . Мы работаем с индексами и перегружаем операцию < таким образом, что сравнения обращаются к элементам клиентского массива. При этом возникают некоторые трудности, поскольку программе обработки очереди с приоритетами приходится отслеживать объекты, чтобы она могла отыскать их, если клиентская программа обращается к ним по дескриптору (индексу массива). C этой целью добавляется второй индексный массив, с помощью которого отслеживается положение ключей в очереди с приоритетами. Для локализации использования этого массива необходимо дать соответствующее определение операции exch и перемещать данные только с ее помощью.

Программа 9.12 является полной реализацией этого подхода на базе пирамидальных деревьев. Она лишь незначительно отличается от программы 9.5, но достойна специального изучения, поскольку очень полезна в практических ситуациях. Будем называть структуру данных, построенную этой программой, индексным пирамидальным деревом (index heap). Данная программа послужит строительным блоком для других алгоритмов в частях V—VII. Как обычно, здесь не включен код проверок на ошибки, и мы предполагаем (например), что индексы никогда не выходят за пределы их диапазона, а пользователь не делает попыток вставить что-либо в полную очередь или удалить что-либо из пустой очереди. Добавление подобного кода не вызовет особых затруднений.

Этот же подход применим для любой очереди с приоритетами, использующей представление в виде массива (например, см. упражнения 9.50 и 9.51). Основной недостаток применения такой косвенной адресации — дополнительный расход памяти. Размер индексных массивов должен быть равным размеру массива данных, тогда как максимальный размер очереди с приоритетами может быть намного меньше.

Возможны другие подходы к построению очереди с приоритетами из готовых данных, хранящихся в массиве, когда клиентская программа создает записи, состоящие из ключа и индекса массива в поле информации, или использует индексный ключ с операцией <, перегруженной в клиентской программе. Тогда если реализация использует представление в виде связного списка, как в программах 9.9 и 9.10 или в упражнении 9.41, то объем памяти, используемой очередью с приоритетами, будет пропорционален максимальному количеству элементов в очереди за все время. Такие методы могут быть предпочтительнее программы 9.12, если нужно экономить память и если очередь с приоритетами должна содержать лишь небольшую часть массива данных.

Сопоставление этого подхода к построению полной реализации очереди с приоритетами с подходом из раздела 9.5 обнаруживает существенные различия в создании АТД. В первом случае (например, программа 9.8) выделение памяти под ключи и ее освобождение, изменение значений ключей и т.п. входят в обязанности реализации очереди с приоритетами. АТД предоставляет клиентской программе дескрипторы элементов данных, а клиент осуществляет доступ к элементам данных только через обращения к программам обработки очередей с приоритетами, передавая эти дескрипторы в качестве параметров. Во втором случае (например, программа 9.12) клиент отвечает за ключи и записи, а программы обработки очереди с приоритетами обращаются к этой информации только через дескрипторы, предоставляемые пользователем (в программе 9.12 это индексы массива). В обоих случаях требуется взаимодействие между клиентской программой и реализацией.

Программа 9.12. Очередь с приоритетами на базе индексного пирамидального дерева

Эта реализация программы 9.11 использует pq в качестве массива индексов для клиентского массива. Например, если в клиентской программе операция < определена для аргументов типа Index, как указано в комментарии перед программой 9.11, то при выполнении сравнения pq[j] с pq[k] в подпрограмме fixUp на самом деле, как и задумано, сравниваются data.grade[pq[j]] и data.grade[pq[j]]. Здесь предполагается, что Index — это класс-оболочка, объект которого может индексировать массивы, так что позицию в пирамидальном дереве, соответствующую значению индекса k, можно хранить в qp[k]. А это позволяет реализовать операции изменить приоритет и извлечь (см. упражнение 9.49 и рис. 9.14). Для всех k пирамидального дерева справедлив инвариант pq[qp[k]] = qp [pq [k] ] = k (см. рис. 9.13).

template <class Item>
class PQ
  { private:
      int N; Index* pq; int* qp;
      void exch(Index i, Index j)
        { int t;
t = qp[i]; qp[i] = qp[j]; qp[j] = t;
pq[qp[i]] = i; pq[qp[j]] = j;
        }
      void fixUp(Index a[], int k);
      void fixDown(Index a[], int k, int N);
    public:
        PQ(int maxN)
        { pq = new Index[maxN+1];
        qp = new int[maxN+1]; N = 0; }
    int empty() const
        { return N == 0; }
    void insert(Index v)
        { pq[++N] = v; qp[v] = N; fixUp(pq, N); }
    Index getmax()
        { exch(pq[1], pq[N]);
fixDown(pq, 1, N-1);
        return pq[N--]; }
    void change(Index k)
        { fixUp(pq, qp[k]); fixDown(pq, qp[k], N); }
  };
        

В данной книге мы обычно поощряем такое взаимодействие, выходящее за пределы механизмов поддержки языков программирования. В частности, хотелось бы, чтобы характеристики производительности реализации соответствовали динамическому сочетанию операций, нужному клиентской программе. Одним из способов достижения такого соответствия является применение реализаций с известными границами производительности в худшем случае, хотя многие задачи можно решить намного проще, сопоставляя требования этих задач к производительности с возможностями простых реализаций.

Упражнения

9.48. Предположим, что массив заполнен ключами E A S Y Q U E S T I O N. Приведите содержимое массивов pq и qp после занесения этих ключей программой 9.12 в первоначально пустое пирамидальное дерево.

9.50. Реализуйте АТД очереди с приоритетами для индексных элементов (см программу 9.11), используя представление очереди с приоритетами в виде упорядоченного массива.

9.51. Реализуйте АТД очереди с приоритетами для индексных элементов (см. программу 9.11), используя представление очереди с приоритетами в виде неупорядоченного массива.

9.52. Пусть имеется массив a из N элементов. Рассмотрим полное бинарное дерево из 2N элементов (представленное в виде массива pq), содержащее индексы из этого массива и обладающее следующими свойствами: (1) для i от 0 до N-1 справедливо равенство pq[N+i]=i и (2) для i от 1 до N-1 справедливо , если , и в противном случае. Такая структура называется турниром индексного пирамидального дерева (index heap tournament), поскольку сочетает свойства индексных пирамидальных деревьев и турниров (см. программу 5.19). Приведите турнир индексного пирамидального дерева, соответствующий ключам E A S Y Q U E S T I O N.

9.53. Реализуйте АТД очереди с приоритетами для индексных элементов (см. программу 9.11), воспользовавшись турниром индексного пирамидального дерева (см. упражнение 9.52).

Рис. 9.14. Изменение приоритета узла в пирамидальном дереве

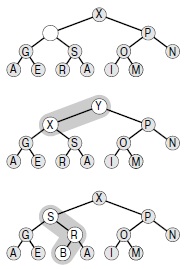
На верхней диаграмме показано дерево, о котором известно, что оно пирамидально упорядочено, за исключением разве что одного узла. Если этот узел больше своего родителя, то его нужно переместить вверх, как показано на рис. 9.3. Эта ситуация показана на средней диаграмме, где узел Y поднимается вверх по дереву (в общем случае его движение может прекратиться и ниже корня). Если узел меньше, чем больший из двух его дочерних узлов, то его нужно переместить вниз по дереву, как показано на рис. 9.3. Эта ситуация показана на нижней диаграмме, где узел B опускается по дереву (в общем случае его движение может прекратиться, не достигнув нижнего уровня). На базе этой процедуры можно реализовать операцию изменить приоритет в пирамидальном дереве, которая позволит восстанавливать пирамидальный порядок после изменения значения ключа в узле, либо операцию извлечь в пирамидальном дереве, которая позволит восстанавливать пирамидальный порядок после замены ключа в узле на самый правый ключ с нижнего уровня дерева.