|
Здравствуйте прошла курсы на тему Алгоритмы С++. Но не пришел сертификат и не доступен.Где и как можно его скаачат? |
Быстрая сортировка
Повторяющиеся ключи
Файлы с большим количеством повторяющихся ключей довольно часто встречаются в различных приложениях. Например, может потребоваться сортировка большого файла с персональными данными по году рождения или даже сортировка для разделения персонала на женщин и мужчин.
Если в сортируемом файле имеется много повторяющихся ключей, рассмотренные нами реализации быстрой сортировки не снижают производительность до неприемлемо низкого уровня, но все же их можно существенно улучшить. Например, файл, который состоит только из одинаковых ключей (одно и то же значение), вообще не нуждается в дальнейшей сортировке, однако наши реализации будут разбивать его до мелких подфайлов, вне зависимости от размера файла (см. упражнение 7.8). Если во входном файле присутствует большое количество повторяющихся ключей, быстрая сортировка, в силу своей рекурсивной природы, обязательно породит много подфайлов, содержащих элементы с одним и тем же ключом, так что здесь имеется возможность для значительного усовершенствования алгоритма.
Идея, которая первой приходит на ум, заключается в разбиении файла на три части, по одной для ключей, меньших, равных и больших центрального элемента:
Выполнение такого разбиения сложнее, чем разбиение на две части, которым мы пользовались ранее. Для решения этой задачи было предложено множество различных методов. Это классическое упражнение по программированию, известное благодаря Дейкстре (Dijkstra) как задача о национальном флаге Дании (Dutch National Flag problem), т.к. трем возможным категориям ключей можно поставить в соответствие три цвета этого флага (см. раздел ссылок). Для быстрой сортировки мы добавим еще одно ограничение: вся работа должна быть выполнена за один проход по файлу - алгоритм, использующий два прохода по данным, замедлит быструю сортировку вдвое, даже если в файле вообще нет повторяющихся ключей.
Интересный метод трехчастного разбиения (three-way partitioning) был предложен в 1993 году Бентли и Макилроем (Bentley and McIlroy). Он представляет собой следующую модификацию стандартной схемы разбиения: помещаем ключи из левого подфай-ла, равные центральному элементу, в левый конец файла, а ключи из правого подфайла, равные центральному элементу - в правый конец файла. Во время процесса разбиения постоянно поддерживается следующая ситуация:
Теперь после перекрещивания индексов уже точно известно, где находятся равные ключи, и мы перемещаем в окончательные позиции все элементы с ключами, равными центральному элементу. Эта схема не совсем удовлетворяет требованию, чтобы трехчастное разбиение файла завершалось за один проход по файлу, но дополнительные издержки для повторяющихся ключей пропорциональны лишь количеству обнаруженных повторяющихся ключей. Из этого факта вытекают два следствия. Во-первых, этот метод хорошо работает, даже если повторяющихся ключей нет, т.к. нет дополнительных издержек. Во-вторых, метод выполняется за линейное время, если имеется лишь постоянное количество значений ключей: каждая фаза разбиения исключает из процесса сортировки все ключи со значениями, равными центральному элементу, так что каждый ключ может участвовать в не более чем постоянном количестве разбиений.
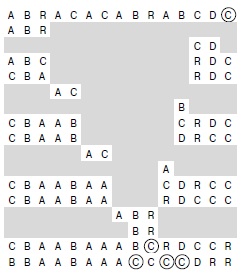
На этой диаграмме показан процесс помещения в окончательные позиции всех ключей, равных центральному элементу. Как и на рис. 7.2, выполняется просмотр с левого конца, пока не будет найден ключ, не меньший центрального, и с правого конца, пока не будет найден ключ, не больший центрального, а затем эти элементы обмениваются. Если после обмена левый элемент равен центральному элементу, он обменивается с элементом на левом конце массива; аналогично и справа. После перекрещивания индексов центральный элемент помещается на свое место как и раньше (предпоследняя строка), а затем выполняется обмен всех ключей, равных ему, чтобы они заняли свои места с любой стороны от центрального элемента (нижняя строка).
На рис. 7.12 показана работа алгоритма трехчастного разбиения на демонстрационном файле, а программа 7.5 является реализацией быстрой сортировки, основанной на описанном методе. Эта реализация требует добавления всего лишь двух операторов if в цикле перестановки и двух циклов for для завершения разбиения, т.е. перемещения ключей, равных центральному элементу, в окончательные позиции. Похоже, что этот метод трехчастного разбиения требует меньшего кода, чем другие альтернативы. И более того, он не только максимально эффективно обрабатывает повторяющиеся ключи, но и минимизирует издержки в случае, когда повторяющихся ключей нет.
Программа 7.5. Быстрая сортировка с трехчастным разбиением
В основу программы положено разбиение массива на три части: на элементы, меньшие центрального элемента (в a[1], ..., a[j]), элементы, равные центральному элементу (в a[j+1], ..., a[i-1]), и элементы, большие центрального элемента (в a[i], ..., a[r]). После этого сортировка завершается двумя рекурсивными вызовами.
Для достижения этой цели программа хранит ключи, равные центральному элементу, слева между позициями l и p и справа между q и r. В цикле разбиения, после остановки индексов просмотра и перестановки элементов в позициях i и j , выполняется проверка каждого из этих элементов на равенство центральному. Если левый из них равен центральному элементу, он переставляется в левую часть массива; если правый из них равен центральному элементу, он переставляется в правую часть массива.
После перекрещивания индексов элементы массива, равные центральному, переставляются с концов в свои окончательные позиции, после чего их можно исключить из подфайлов, обрабатываемых рекурсивными вызовами.
template <class Item>
int operator==(const Item &A, const Item &B)
{ return !less(A, B) && !less(B, A); }
template <class Item>
void quicksort(Item a[], int l, int r)
{ int k; Item v = a[r];
if (r <= l) return;
int i = l-1, j = r, p = l-1, q = r;
for (;;)
{
while (a[++i] < v) ;
while (v < a[--j]) if (j == l) break;
if (i >= j) break;
exch(a[i],a[j]);
if (a[i] == v) { p++; exch(a[p],a[i]); }
if (v == a[j]) { q-; exch(a[q],a[j]); }
}
exch(a[i], a[r]); j = i-1; i = i+1;
for (k = l ; k <= p; k++, j -) exch(a[k],a[j]);
for (k = r-1; k >= q; k--, i++) exch(a[k],a[i]);
quicksort(a, l, j);
quicksort(a, i, r);
}
Упражнения
7.34. Поясните, что произойдет, если программа 7.5 будет запущена для случайно упорядоченного файла (1) с двумя различными значениями ключей и (2) с тремя различными значениями ключей.
7.35. Измените программу 7.1 так, чтобы выполнялась команда return, если все ключи в подфайле равны. Сравните эффективность полученной программы с программой 7.1 для больших случайно упорядоченных файлов с ключами, принимающими t различных значений для t = 2, 5 и 10.
7.36. Предположим, в программе 7.2 просмотр не останавливается на ключах, равных центральному, а пропускает их. Покажите, что в этом случае время выполнения программы 7.1 будет квадратичным.
7.37. Докажите, что время выполнения программы из упражнения 7.36 квадратично для всех файлов с 0(1) различными значениями ключей.
7.38. Напишите программу для определения количества различных ключей, встречающихся в файле. Воспользуйтесь полученной программой для подсчета различных ключей в случайно упорядоченных файлах, содержащих N целых чисел из диапазона от 0 до M- 1 для M = 10, 100 и 1000 и для N = 103, 104, 105 и 106 .
Строки и векторы
Когда ключами сортировки являются строки, можно воспользоваться реализацией типа данных наподобие программы 6.11 совместно с реализациями быстрой сортировки из данной главы. В результате получится корректная и эффективная реализация (для больших файлов быстрее любого другого рассмотренного нами метода), но в ней будут присутствовать неявные издержки, которые стоит рассмотреть подробнее.
Проблема заключается в затратах на сравнение строк. Обычно строки сравниваются слева направо, проверяя на равенство символ за символом и затрачивая на это время, пропорциональное количеству начальных символов, совпадающих в обеих строках. На заключительных стадиях разбиения быстрой сортировки, когда ключи близки по значению, сравнение может быть относительно долгим. Как обычно, в силу рекурсивного характера быстрой сортировки, почти все затраты алгоритма сосредоточены в его завершающих стадиях, так что попытки усовершенствования алгоритма вполне оправданы.
Например, рассмотрим подфайл размером 5, содержащий ключи discreet, discredit, discrete, discrepancy и discretion. Все сравнения при сортировке этих ключей проверяют по меньшей мере семь символов, в то время как достаточно начать с седьмого символа - если бы дополнительно было известно, что первые шесть символов совпадают.
Процедура трехчастного разбиения, рассмотренная в разделе 7.6, обеспечивает элегантный способ использовать это соображение. На каждой стадии разбиения проверяется лишь один символ (скажем, символ в позиции d), считая, что сортируемые ключи совпадают в позициях с 0 по d-1. Мы выполняем трехчастное разбиение, помещая те ключи, у которых d-й символ меньше d-го символа центрального элемента, слева, ключи, d-й символ которых равен d-му символу центрального элемента, в середине; а ключи, d-й символ которых больше d-го символа центрального элемента, справа. Далее продолжаем как обычно, за исключением того, что мы сортируем средний подфайл, начиная с d+1-го символа. Нетрудно видеть, что этот метод обеспечивает корректную сортировку и к тому же оказывается очень эффективным (см. таблица 7.2). Это убедительный пример мощи рекурсивного мышления (и программирования).
В таблица 7.2 представлены относительные затраты для нескольких различных вариантов быстрой сортировки на примере упорядочения первых N слов из книги Г Мелвилла " Моби Дик " . Использование сортировки вставками непосредственно для небольших подфайлов или их игнорирование с последующей сортировкой вставками являются эквивалентными по эффективности стратегиями, но снижение затрат здесь несколько ниже, чем для целочисленных ключей (см. таблица 7.1), т.к. сравнение строк более трудоемко. Если во время разбиения файлов не останавливаться на повторяющихся ключах, тогда время сортировки файла со всеми одинаковыми ключами квадратично. Эта неэффективность видна в приведенном примере, т.к. в тексте есть много слов, встречающихся с большой частотой. По этой причине эффективно трехчастное разбиение, которое на 30-35% быстрее системной сортировки.
| N | V | I | M | Q | X | T |
|---|---|---|---|---|---|---|
| 12500 | 8 | 7 | 6 | 10 | 7 | 6 |
| 25000 | 16 | 14 | 13 | 20 | 17 | 12 |
| 50000 | 37 | 31 | 31 | 45 | 41 | 29 |
| 100000 | 91 | 78 | 76 | 103 | 113 | 68 |
| Обозначения: | |
|---|---|
| V | Быстрая сортировка (программа 7.1) |
| I | Сортировка вставками для подфайлов небольших размеров |
| M | Игнорирование небольших подфайлов с последующей сортировкой вставками |
| Q | Системная сортировка qsort |
| X | Пропуск повторяющихся ключей (квадратичное время для всех равных ключей) |
| T | Трехчастное разбиение (программа 7.5) |
Для реализации этого вида сортировки требуется более общий абстрактный тип данных, обеспечивающий доступ к отдельным символам ключей. Способ обработки строк в C++ позволяет исключительно просто реализовать этот метод. Однако мы отложим детальное обсуждение этой реализации до "Поразрядная сортировка" , в которой рассмотрим различные методы сортировки, использующие то обстоятельство, что ключи сортировки могут быть легко расчленены на более мелкие части.
Этот подход можно распространить на многомерные сортировки, где ключами сортировки являются векторы, а записи должны быть отсортированы таким образом, что ключи упорядочены по первой компоненте, а записи с равными первыми компонентами ключей упорядочены по второй компоненте и т.д. Если компоненты не содержат повторяющихся ключей, задача сводится к сортировке по первой компоненте; однако в типичных приложениях каждая из компонент может принимать лишь нескольких различных значений, и поэтому применимо трехчастное разбиение (переходящее к следующей компоненте в среднем подфайле). Этот случай имеет важное практическое применение, рассмотренное Хоаром (Hoare) в его оригинальной работе.
Упражнения
7.39. Рассмотрите возможность усовершенствования сортировки выбором, сортировки вставками, пузырьковой сортировки и сортировки Шелла для упорядочения строк.
7.40. Сколько символов проверяет стандартный алгоритм быстрой сортировки (программа 7.1, использующая строковый тип из программы 6.11) при сортировке файла, состоящего из одинаковых N строк длиной t ? Ответьте на этот же вопрос для модификации, предложенной в тексте.