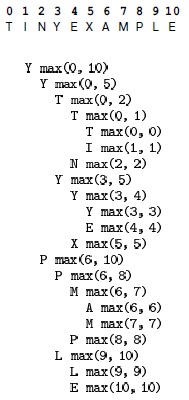Рекурсия и деревья

Программа 5.4. Рекурсивная программа для вычисления префиксных выражений

Для вычисления префиксного выражения либо осуществляется преобразование числа из ASCII в двоичную форму (в цикле while в конце программы), либо выполняется операция, указанная первым символом выражения, с двумя операндами, которые вычисляются рекурсивно. Эта функция является рекурсивной, однако использует глобальный массив, содержащий выражение и индекс текущего символа выражения. Индекс увеличивается после вычисления каждого подвыражения.

char *a; int i;
int eval()
  { int x = 0;
    while (a[i] == ' ') i++;
    if (a[i] == ' + ')
      { i++; return eval() + eval(); }
    if (a[i] == '*')
      { i++; return eval() * eval(); }
    while ((a[i] >= '0') && (a[i] <= '9'))
      x = 10*x + (a[i++] -'0');
    return x;
  }
        

В принципе, любой цикл for можно заменить эквивалентной рекурсивной программой. Часто рекурсивная программа предоставляет более естественный способ выражения вычисления, чем цикл for, поэтому можно воспользоваться преимуществами механизма, предоставляемого системой с поддержкой рекурсии. Однако следует помнить, что здесь имеются скрытые издержки. Как должно быть понятно из примеров, приведенных на рис. 5.3 при выполнении рекурсивной программы вызовы функций вкладываются один в другой, пока не будет достигнута точка, где вместо рекурсивного вызова выполняется возврат. В большинстве сред программирования такие вложенные вызовы функций реализуются с помощью эквивалента встроенных стеков. В данной главе мы рассмотрим сущность подобного рода реализаций. Глубина рекурсии - это максимальная степень вложенности вызовов функций в ходе вычисления. В общем случае глубина зависит от входных данных. Например, глубина рекурсии в примерах, приведенных на рис. 5.2 и рис. 5.3, составляет, соответственно, 9 и 4. бедует учитывать, что для работы рекурсивной программы среда программирования задействует стек, размер которого пропорционален глубине рекурсии. При решении сложных задач необходимый для этого стека объем памяти может заставить отказаться от использования рекурсивного решения.

Рис. 5.3. Пример вычисления префиксного выражения

Эта вложенная последовательность вызовов функций иллюстрирует работу рекурсивного алгоритма вычисления префиксного выражения. Для простоты здесь показаны аргументы выражения. Сам по себе алгоритм никогда явно не определяет длину строки своих аргументов: вся необходимая информация содержится в начале строки.

Огруктуры данных, построенные из узлов с указателями, рекурсивны по своей природе. Например, рекурсивным является определение связных списков в "Элементарные структуры данных" (определение 3.3). Cледовательно, рекурсивные программы обеспечивают естественные реализации для многих часто используемых функций, работающих с этими структурами данных. Программа 5.5 содержит четыре таких примера. Подобные реализации в книге используются часто - в основном потому, что их гораздо проще понять, чем их нерекурсивные аналоги. Однако при обработке очень больших списков рекурсивные программы, подобные программе 5.5, следует использовать с осторожностью, поскольку глубина рекурсии для таких функций может быть пропорциональна длине списков и, соответственно, требуемый для рекурсивного стека объем памяти может оказаться слишком большим.

Некоторые среды программирования автоматически выявляют и исключают концевую рекурсию (tail recursion), когда последним действием функции является рекурсив -

ный вызов, т.к. в этом случае увеличение глубины рекурсии вовсе не обязательно. Это усовершенствование преобразовало бы функции подсчета, обхода и удаления, используемые в программе 5.5, в циклы, но оно не применимо к функции обхода в обратном направлении.

В разделах 5.2 и 5.3 будут рассмотрены два семейства рекурсивных алгоритмов, представляющие важные вычислительные парадигмы. Затем, в разделах 5.4 - 5.7, мы познакомимся с рекурсивными структурами данных, служащими основой для большой группы алгоритмов.

Программа 5.5. Примеры рекурсивных функций для связных списков

Эти рекурсивные функции для выполнения простых задач обработки списков легко записать, но они могут оказаться бесполезными для очень больших списков, поскольку глубина рекурсии может быть пропорциональна длине списка.

Первая функция, count, подсчитывает количество узлов в списке. Вторая, traverse, вызывает функцию visit для каждого узла списка, с начала до конца. Обе функции легко реализуются и с помощью цикла for или while. Третья функция, traverseR, не имеет простого итеративного аналога. Она вызывает функцию visit для каждого узла списка, но в обратном порядке.

Четвертая функция, remove, удаляет из списка все узлы с заданным значением элемента. Реализация этой функции основана на изменении ссылки x = x ->next в узлах, предшествующих удаляемым, что возможно благодаря использованию ссылочного параметра. Структурные изменения для каждой итерации цикла while совпадают с показанными на рис. 3.3, но в данном случае и x, и t указывают на один и тот же узел.

int count(link x)
  {
    if (x == 0) return 0;
    return 1 + count(x ->next);
  }
void traverse(link h, void visit(link))
  {
    if (h == 0) return;
    visit(h);
    traverse(h ->next, visit);
  }
void traverseR(link h, void visit(link))
  {
    if (h == 0) return;
    traverseR(h ->next, visit); visit(h);
  }
void remove(link& x, Item v)
  {
    while (x != 0 && x ->item == v)
      { link t = x; x = x ->next; delete t; }
    if (x != 0) remove(x ->next, v);
  }
        

Упражнения

5.1. Напишите рекурсивную программу для вычисления lg(N!).

5.2. Измените программу 5.1 для вычисления N! mod M без риска вызвать переполнение. Попробуйте выполнить программу для M = 997 и N = 10³, 10⁴, 10⁵ и 10⁶ , чтобы увидеть, как используемая система программирования обрабатывает рекурсивные вызовы с большой глубиной вложенности.

5.3. Приведите последовательности значений аргумента, получаемых в результате вызова программы 5.2 для каждого из целых чисел от 1 до 9.

5.4. Найдите значение N < 106 , при котором программа 5.2 выполняет максимальное количество рекурсивных вызовов.

5.5.Создайте нерекурсивную реализацию алгоритма Евклида.

5.6. Приведите рисунок, соответствующий рис. 5.2, для результата выполнения алгоритма Евклида с числами 89 и 55.

5.7. Определите глубину рекурсии алгоритма Евклида для двух последовательных чисел Фибоначчи (F_N и F_N+1) .

5.8. Приведите рисунок, соответствующий рис. 5.3, для результата вычисления префиксного выражения + * * 12 12 12 144.

5.9. Напишите рекурсивную программу для вычисления постфиксных выражений.

5.10. Напишите рекурсивную программу для вычисления инфиксных выражений, в которых операнды всегда заключены в круглые скобки.

5.11. Напишите рекурсивную программу, которая преобразует инфиксные выражения в постфиксные.

5.12. Напишите рекурсивную программу, которая преобразует постфиксные выражения в инфиксные.

5.13. Напишите рекурсивную программу для решения задачи Иосифа Флавия (см. "Элементарные структуры данных" ).

5.14. Напишите рекурсивную программу, которая удаляет последний узел из связного списка.

5.15. Напишите рекурсивную программу для изменения порядка следования узлов в связном списке на обратный (см. программу 3.7). Совет: используйте глобальную переменную.

Разделяй и властвуй

Во множестве рассматриваемых в книге программ используются два рекурсивных вызова, каждый из которых работает приблизительно с половиной входных данных. Эта рекурсивная схема - вероятно, наиболее важный случай хорошо известного метода "разделяй и властвуй ", который служит основой для разработки важнейших алгоритмов.

В качестве примера рассмотрим задачу отыскания максимального из N элементов массива a[0], ..., a[N -1]. Эту задачу можно легко выполнить за один проход по массиву:

for (t = a[0], i = 1; i < N; i++)
  if (a[i] > t) t = a[i];
        

Рекурсивное решение типа "разделяй и властвуй ", приведенное в программе 5.6 - также простой (хотя и совершенно иной) алгоритм решения той же задачи; он приведен только для иллюстрации концепции "разделяй и властвуй ".

Часто подход "разделяй и властвуй " обеспечивает более быстрые решения, чем простые итерационные алгоритмы (в конце раздела мы рассмотрим несколько примеров); кроме того, данный подход заслуживает внимательного изучения, поскольку помогает понять суть некоторых фундаментальных вычислений.

Рис. 5.4. Рекурсивный способ отыскания максимума

Эта последовательность вызовов функций иллюстрирует динамику отыскания максимума с помощью рекурсивного алгоритма.

На рис. 5.4 показаны рекурсивные вызовы, выполняемые при запуске программы 5.6 для некоторого массива. Структура последовательности вызовов кажется сложной, но обычно об этом можно не беспокоиться - для доказательства правильности работы программы мы полагаемся на метод математической индукции, а для анализа ее производительности используется рекуррентное соотношение.

Как обычно, сам код предлагает проверку правильности вычисления методом индукции:

• Он явно и немедленно находит максимальный элемент массива, размер которого равен 1.
• Для N > 1 код разделяет массив на два, размер каждого из которых меньше N, исходя из индуктивного предложения, находит максимальные элементы в обеих частях и возвращает большее из этих двух значений, которое должно быть максимальным значением для всего массива.

Более того, рекурсивную структуру программы можно использовать для исследования характеристик ее производительности.

Программа 5.6. Применение принципа "разделяй и властвуй " для отыскания максимума

Эта функция делит массив a[l] , ..., a[r] на массивы a[l] , ..., a[m] и a[m+1], ..., a[r], находит (рекурсивно) максимальные элементы в обеих частях и возвращает больший из них в качестве максимального элемента всего массива. Предполагается, что Item - тип первого класса, для которого операция определена >. Если размер массива является четным числом, обе части имеют одинаковые размеры, а если нечетным, эти размеры различаются на 1.

Item max(Item a[], int l, int r)
  {
    if (l == r) return a[l] ;
    int m = (l+r) /2;
    Item u = max(a, l, m);
    Item v = max(a, m+1, r);
    If (u > v) return u; else return v;
  }
        

Программа 5.6 - типичный пример для многих алгоритмов вида "разделяй и властвуй ", имеющих совершенно одинаковую рекурсивную структуру, но другие примеры могут отличаться от приведенного в двух аспектах. Во-первых, программа 5.6 выполняет одинаковый объем вычислений для каждого вызова функции, и поэтому ее общее время выполнения линейно. Как мы увидим, другие алгоритмы "разделяй и властвуй " могут выполнять различный объем вычислений для различных вызовов функций, и поэтому для определения общего времени выполнения требуется более сложный анализ. Время выполнения таких алгоритмов зависит от конкретного способа разделения на части. Во -вторых, программа 5.6 - типичный пример алгоритмов "разделяй и властвуй ", для которых сумма размеров частей равна размеру общей задачи. Другие алгоритмы "разделяй и властвуй " могут делить задачу на части, сумма размеров которых меньше или больше размера исходной задачи. Эти алгоритмы тоже относятся к рекурсивным алгоритмам "разделяй и властвуй ", поскольку каждая часть меньше целого, но анализировать их труднее, чем программу 5.6. Мы подробно проанализируем каждый из этих видов алгоритмов по мере их рассмотрения.

Например, алгоритм бинарного поиска, приведенный в разделе 2.6 "Принципы анализа алгоритмов" , является алгоритмом вида "разделяй и властвуй ", который делит задачу пополам, а затем работает только с одной из этих половин. Рекурсивная реализация бинарного поиска будет рассмотрена в "Таблицы символов и деревья бинарного поиска" .

На рис. 5.5 показано содержимое внутреннего стека, который используется средой программирования для реализации вычислений, изображенных на рис. 5.4. Приведенная на рисунке модель является идеализированной, но она позволяет понять структуру вычисления по методу "разделяй и властвуй ". Если в программе имеются два рекурсивных вызова, то во время ее выполнения внутренний стек содержит сначала один элемент, соответствующий первому вызову функции во время выполнения (он содержит значения аргументов, локальные переменные и адрес возврата), а затем аналогичный элемент для второго вызова функции. На рис. 5.5 показан другой подход - помещение в стек сразу двух элементов с сохранением всех подстеков, которые должны явно создаваться в стеке. Такая организация проясняет структуру вычислений и закладывает основу для более общих вычислительных схем, подобных тем, о которых пойдет речь в разделах 5.6 и 5.8.

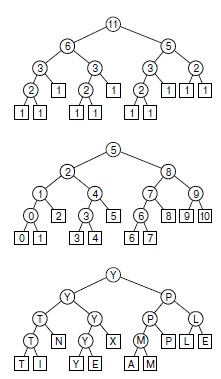
На рис. 5.6 показана структура алгоритма "разделяй и властвуй " для поиска максимального значения. Эта структура является рекурсивной: верхний узел содержит размер входного массива; структура левого подмассива изображена слева, а правого - справа. Формальное определение и описание структур деревьев такого вида приведены в разделах 5.4 и 5.5. Они облегчают понимание структуры любых программ, в которых используются вложенные вызовы функций, но особенно рекурсивных программ.

Рис. 5.5. Пример динамики внутреннего стека

Здесь изображено идеализированное представление содержимого внутреннего стека во время вычисления примера из рис. 5.4. Обработка начинается с занесения в стек левого и правого индексов всего подмассива. Каждая строка представляет результат занесения в стек двух индексов и, если они не равны, вталкивания четырех индексов, которые ограничивают левый и правый подмасивы после разделения вытолкнутого подмассива на две части. На практике вместо таких действий система хранит в стеке адреса возврата и локальные переменные, однако эта модель вполне адекватно описывает вычисление.

Рис. 5.6. Рекурсивная структура алгоритма поиска максимума

Алгоритм "разделяй и властвуй "разбивает задачу размером 11 на задачи с размерами 6 и 5, задачу размером 6 - на две задачи с размерами 3 и 3 - и т.д., пока не будет получена задача размером 1 (вверху). Каждый кружок на этих диаграммах означает вызов рекурсивной функции для расположенных непосредственно под ней узлов, связанных с ней линиями (квадратики означают вызовы, в которых рекурсия завершается). На диаграмме в центре показано значение индекса в середине разбиения файла; на нижней диаграмме показано возвращаемое значение.

На рис. 5.6 внизу показано такое же дерево, но в нем каждый узел содержит значение, возвращаемое соответствующим вызовом функции. Процесс создания связных структур, которые представляют подобные деревья, рассматривается в разделе 5.7.

Ни одно рассмотрение рекурсии не будет полным без рассмотрения старинной задачи о ханойских башнях. Имеется три стержня и N дисков, которые помещаются на трех стержнях. Диски различаются размерами и вначале размещаются на одном из стержней от самого большого (диск N) внизу до самого маленького (диск 1) вверху. Задача состоит в перемещении дисков на соседнюю позицию (стержень) при соблюдении следующих правил: (1) одновременно можно переложить только один диск; и (2) ни один диск нельзя положить на диск меньшего размера. Легенда гласит, что конец света наступит тогда, когда некая группа монахов выполнит такую задачу для 40 золотых дисков на трех алмазных стержнях.

Программа 5.7 предоставляет рекурсивное решение этой задачи. Она указывает диск, который должен быть перемещен на каждом шагу, и направление его перемещения (+ означает перемещение на один стержень вправо, или на крайний левый, если текущий стержень крайний справа, а - означает перемещение на один стержень влево, или на крайний правый, если текущий стержень крайний слева). Рекурсия основана на следующей идее: для перемещения N дисков вправо на один стержень нужно вначале верхние N - 1 дисков переместить на один стержень влево, затем переложить диск N на один стержень вправо, и потом переложить N - 1 дисков еще на один стержень влево (поверх диска N). Правильность этого решения можно доказать по индукции. На рис. 5.7 показаны перемещения для N = 5 и рекурсивные вызовы для N = 3. Структура алгоритма достаточно очевидна; давайте рассмотрим его подробно.