Численные методы решения уравнений в частных производных
[+]
Опубликован: 25.10.2007 | Доступ: свободный | Студентов: 1279 / 290 | Оценка: 4.40 / 4.36 | Длительность: 21:57:00
Темы: Алгоритмы и дискретные структуры, Математика
Специальности: Математик
Теги: beta, алгоритмы, вторая производная, вычисления, диффузия, задача Коши, законы, искусственная жизнь, исследования, моделирование, невязка, обыкновенное дифференциальное уравнение, однородное уравнение, параллельные вычисления, потоки, собственный вектор, уравнения газовой динамики, уравнениями в частных производных, численное решение уравнений, элементы

Лекция 5: Численное решение уравнений в частных производных гиперболического типа с большими градиентами решений

A
|
версия для печати
< Лекция 4 || Лекция 5: 123456789 || Лекция 6 >

5.9. TVD - схемы для квазилинейного уравнения с антидиффузией.

Повысить порядок аппроксимации TVD - схем можно, введя в уравнение переноса антидиффузионный член

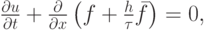
$ \frac{{\partial}u}{{\partial}t} + \frac{{\partial}}{{\partial}x} \left( {f + \frac{h}{\tau} \bar{f}}\right) = 0, $

где дополнительный антидиффузионный поток имеет порядок погрешности аппроксимации и вводится по формуле

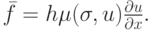
$ \bar{f} = h {\mu}({\sigma}, u) \frac{{\partial}u}{{\partial x}}. $

Очевидно, что это дополнительное слагаемое в исходном уравнении будет иметь вид

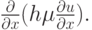
$ \frac{{\partial}}{{\partial}x}(h {\mu}\frac{{\partial}u} {{\partial}x}). $

Таким образом, проведена коррекция потока, компенсирована аппроксиммационная вязкость. Хартен предложил модифицировать поток, введя в него функцию P:

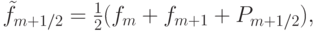
$ \tilde{f}_{m + 1/2} = \frac{1}{2}(f_m + f_{m + 1} + P_{m + 1/2} ), $

причем разные TVD - схемы различаются выбором этого слагаемого P. В исходном варианте разностной схемы, предложенной Хартеном, эта функция выбиралась следующим образом:

$ P_{m + 1/2} = \frac{h}{\tau}(\bar{f}_m + \bar{f}_{m + 1} - \left|{\xi_{m + 1/2} + \bar{\xi}_{m + 1/2}}\right| \Delta_{m + 1/2} u), $

где \xi _{m + 1/2} = \sigma a_{m + 1/2},

$ \bar{f}_{m \pm 1/2} = \frac{1}{2} \left({\left| {\xi_{m + 1/2}}\right| - \xi_{m + 1/2}^2}\right) \Delta_{m + 1/2}u. $

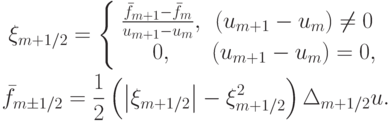
\begin{gather*} \xi_{m + 1/2} = \left\{ \begin{array}{cc} {\frac{\bar{f}_{m + 1} - \bar{f}_m}{u_{m + 1} - u_m}, } & {(u_{m + 1} - u_m) \ne 0} \\ {0, } & {(u_{m + 1} - u_m) = 0, } \\ \end{array} \right. \\ \bar{f}_{m \pm 1/2} = \frac{1}{2} \left(\left| \xi_{m + 1/2}\right| - \xi^2_{m + 1/2}\right) \Delta_{m + 1/2}u. \end{gather*}

Эта схема, тем не менее, приводила к заметному размазыванию разрывов в решении.

Приведем также другие виды ограничительной функции. Общий вид записи лимитера будет один и тот же:

P_{m + 1/2} = - \left[{{\sigma}Q_{m + 1/2} + \eta (a_{m + 1/2})(\Delta_{m + 1/2} u - Q_{m + 1/2} )}\right],

а Qm + 1/2 может выбираться из следующих вариантов:

\begin{gather*} Q_{m + 1/2} = \min\bmod (\Delta_{m + 1/2} u, \Delta_{m - 1/2} u) + \\ + \min\bmod (\Delta_{m + 1/2} u, \Delta_{m + 3/2} u) - \Delta_{m + 1/2}, \\ Q_{m + 1/2} = \min\bmod (\Delta_{m - 1/2} u, \Delta_{m + 1/2}u, \Delta_{m + 3/2} u), \\ Q_{m + 1/2} = \min\bmod (2 \Delta_{m - 1/2} u, 2 \Delta_{m + 1/2} u), 2 \Delta_{m + 3/2} u, 0, 5(\Delta_{m + 3/2} u + \Delta_{m - 1/2})). \end{gather*}

Еще один вариант выбора лимитера в уравнении квазилинейного типа будет

P_{m + 1/2} = - \left[{{\sigma}(a_{m + 1/2}^2 ) \tilde{Q}_{m + 1/2} + \eta (a_{m + 1/2} )(1 - \bar{Q}_{m + 1/2} )}\right] \Delta_{m + 1/2} u,

С согласованным выбором функции 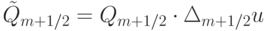\tilde{Q}_{m + 1/2} = Q_{m + 1/2} \cdot \Delta_{m + 1/2} u.

Введем обозначения показателей локальной гладкости решения

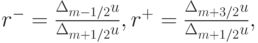
$ r^{-} = \frac{{\Delta_{m - 1/2} u}}{{\Delta_{m + 1/2} u}}, r^{+} = \frac{{\Delta_{m + 3/2} u}}{{\Delta_{m + 1/2} u}}, $

и представим функции Q(r -, r +), входящие в выражения для ограничения потока, в виде

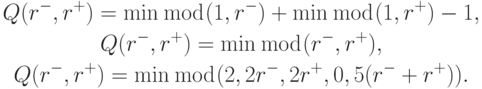
\begin{gather*} Q(r^{-}, r^{+}) = \min\bmod(1, r^{-}) + \min\bmod(1, r^{+}) - 1, \\ Q(r^{-}, r^{+}) = \min\bmod(r^{-}, r^{+}), \\ Q(r^{-}, r^{+}) = \min\bmod(2, 2r^{-}, 2r^{+}, 0, 5(r^{-}+ r^{+}) ). \end{gather*}

Итак, напомним основные идеи, направленные на построение TVD - схем повышенного порядка точности:

  • - построение гибридных схем, аналогичных методу коррекции потоков [15.17];
  • - построение схем с модифицированным по Хартену потоком [15.18];
  • - построение схем, основанных на методе Годунова второго порядка аппроксимации [15.20], [15.21].
Дальше >>
< Лекция 4 || Лекция 5: 123456789 || Лекция 6 >

Вопросы и ответы

вопросов: 0