Лекция 5: Численное решение уравнений в частных производных гиперболического типа с большими градиентами решений
5.6. ENO - схемы
Рассмотрим построение схемы типа ENO, предложенной в [15.4], для уравнения переноса. Основная идея этих схем заключается в использовании двух (или более) шаблонов для обеспечения двух традиционно противоположных свойств: второго (или третьего) порядка точности и монотонности без наличия аппроксимационной или искусственной вязкости. Обычно используются две базовые схемы: с центральными и односторонними разностями, а также с условием переключения, зависящим от значения производных (первой и второй) и знака скорости переноса.
Рассмотрим один из вариантов построения этого метода, для численного решения линейного уравнения переноса. Запишем схему в потоковой форме

а сами числовые потоки будем вычислять по формулам, в которые введем неопределенные пока коэффициенты:

Выпишем первое дифференциальное приближение (ПДП) разностной схемы ( "Численные методы решения уравнений в частных производных гиперболического типа (на примере уравнения переноса)" ). Для этого выпишем проекцию точного решения уравнения переноса на введенную разностную сетку, разложим в ряды Тейлора в окрестности любой точки шаблона и приведем подобные слагаемые. В получившемся дифференциальном уравнении оставим главные члены невязки. Кроме того, как более информативную, рассматриваем П - форму, после всех вычислений получим
![$ \frac{{\partial}u}{{\partial}t} + a \frac{{\partial}u}{{\partial}x} =
\left[{\frac{h}{2} \left| a\right|(1 + 2{\alpha} - 2{\beta}) - \frac{{{\tau}a^2}}{2}}\right] \frac{{{\partial}^2 u}}{{{\partial}x^2}}. $](/sites/default/files/tex_cache/6929f8f3dfee798665127c2b73d0fd77.png)
Из ПДП следует, что при  получаем схему первого
порядка, при
получаем схему первого
порядка, при  — второго порядка с центральными разностями,
— второго порядка с центральными разностями,

Потребуем, чтобы коэффициент при второй производной в первом дифференциальном приближении схемы с центральными разностями обратился в нуль. Это означает, что в схеме отсутствует схемная (аппроксимационная) вязкость. Отсюда получим

Если ввести аналог числа Куранта

 .
.Для схем с ориентированными разностями (  ) условие
равенства нулю аппроксимационной вязкости дает
) условие
равенства нулю аппроксимационной вязкости дает

Исследование обеих схем на монотонность, которое здесь опускается, приводит к условиям



Можно выделить монотонные разностные схемы без аппроксимационной вязкости, если реализовать переключение с одной схемы на другую.
Для такой монотонной схемы можно выписать окончательный вид потоков. Формулы для потоков выпишем через число Куранта.

если

если

Здесь применяются обозначения 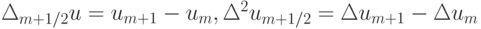 .
.
