Лекция 5: Численное решение уравнений в частных производных гиперболического типа с большими градиентами решений
5.8. Однопараметрическое семейство неявных схем
Рассмотрим однопараметрическое семейство неявных разностных схем для численного решения нелинейного уравнения переноса. Схемы, принадлежащие этому семейству, запишутся следующим образом:

весовой множитель меняется от нуля до единицы: 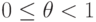 .
.
Потоковая форма записи этих квазилинейных уравнений будет
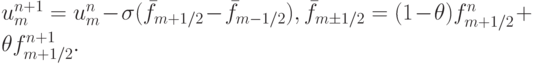
Такая запись однопараметрического семейства схем включает в себя как явные
(при  ), так и неявные (например, при
), так и неявные (например, при 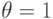 ,
, 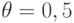 ) разностные схемы.
) разностные схемы.
Для вычисления числового потока будем использовать формулы
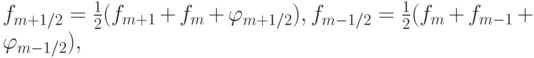
где дополнительные слагаемые для вычисления потока в полуцелых точках есть
![\begin{gather*}
\varphi_{{m} + 1/2} = - \Delta_{{m} + 1/2} u \left[{\eta (a_{{m} + 1/2} )(1 - Q_{{m} + 1/2} ) + \sigma_{{m} - 1/2}^2 Q_{{m} + 1/2}}\right], \\
\varphi_{{m} - 1/2} = - \Delta_{{m} - 1/2} u \left[{\eta (a_{{m} - 1/2} )(1 - Q_{{m} - 1/2} ) + \sigma_{{m} - 1/2}^2 Q_{{m} - 1/2}}\right]. \end{gather*}](/sites/default/files/tex_cache/7f1b66d0f4684e3371ce7c52a134bbb7.png)
Подстановка выражений для потоков в исходную однопараметрическую разностную схему приводит к следующему выражению:
![\begin{gather*}
u_m^{n + 1} + \frac{{\sigma}}{2} \theta \left\{{f_{{m} + 1} - \left[{\eta (a_{{m} + 1/2} )(1 - Q_{{m}+ 1/2} )+ \sigma_{{m} + 1/2}^2 Q_{{m} + 1/2}}\right] \Delta_{{m} + 1/2}
u}\right\}^{n + 1} - \\
- \frac{{\sigma}}{2} \theta \left\{{f_{m - 1} - \left[{\eta (a_{{m} - 1/2} ) (1 - Q_{{m}{- } 1/2} ) + \sigma_{{m} - 1/2}^2 Q_{{m} - 1/2}}\right] \Delta_{{m} - 1/2} u}\right\}^{n + 1} = F_m^{n}, \end{gather*}](/sites/default/files/tex_cache/b7dd06b1a5317ea003bbaf043534c8d0.png)
или
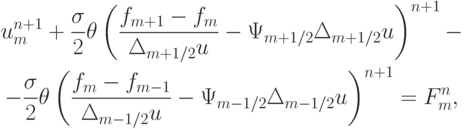
где 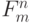 — величины, вычисляемые на n
слое по времени, кроме того, в левой части прибавили и вычли величину
— величины, вычисляемые на n
слое по времени, кроме того, в левой части прибавили и вычли величину  , введено обозначение
, введено обозначение 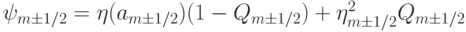 .
.
При способе вычисления локальной скорости переноса в соответствии с правилами
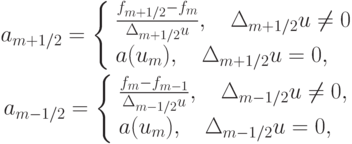
получим разностную схему
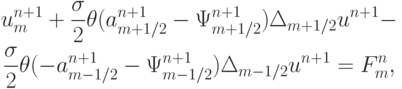
или, в чуть сокращенной форме записи,

Алгоритм решения приведенного разностного уравнения — прогонка.
