Лекция 2: Численное решение дифференциальных уравнений в частных производных параболического типа на примере уравнения теплопроводности
2.2. Разностные схемы для численного решения нелинейного уравнения теплопроводности
2.2.1. Неявная схема с нелинейностью на нижнем слое
![$ \frac{{u_m^{n + 1} - u_m^{n}}}{\tau} = \frac{1}{h} \left[{a_{n + 1\2} \frac{u_{m + 1}^{n + 1} - u_m^{n + 1}}{h} - a_{n - 1\2}} \frac{u_m^{n + 1} - u_{m - 1}^{n + 1}}{h}}\right] + f_m^{n}, $](/sites/default/files/tex_cache/6be72766a80a99c19bb5aa95bc715df1.png)
где am + 1/2 вычисляется следующим образом:
На верхнем слое по времени решение находится с помощью метода прогонки.
Недостаток схемы заключается в необходимости выполнения условия, ограничивающего шаг по времени:  .
.
2.2.2. Схема с нелинейностью на верхнем слое
(необходимость ее реализации появляется, когда условие  оказывается трудновыполнимым):
оказывается трудновыполнимым):

Для реализации алгоритма прогонки проведем линеаризацию функции в правой части, то есть используем итерационный метод Ньютона в функциональных пространствах (метод квазилинеаризации). Пусть  есть i приближение к
есть i приближение к 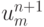 ; необходимо вычислить
; необходимо вычислить 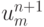 .
.
Тогда
![\begin{gather*}
f(u_m^{i + 1} ) = f[u_m^{i} + (u_m^{i + 1} - u_m^{i} )] \approx f(u_m^{i} ) + f^{\prime}_u (u_m^{i} ) (u_m^{i + 1} - u_m^{i} ), \\
a(u_m^{i + 1} ) = a[u_m^{i} + (u_m^{i + 1} - u_m^{i} )] \approx a (u_m^{i} ) + a^{\prime}_u (u_m^{i} ) (u_m^{i + 1} - u_m^{i} ).
\end{gather*}](/sites/default/files/tex_cache/c01d7f1d077748104f80cc223507da0c.png)
Для вычисления значений сеточной функции на следующем временном слое имеем СЛАУ с трехдиагональной матрицей:

Итерации продолжаются до выполнения условия

При реализации шеститочечной схемы с переменным коэффициентом теплопроводности и нелинейной правой частью f(u) итерационный процесс может иметь следующий вид:
![\begin{gather*}
\frac{{u_m^{i + 1} - u_m^{n}}}{\tau} - \frac{1}{{2h}} \left[{\left({a_{i + 1/2}^{n} \frac{{u_{m + 1}^{i + 1} - u_m^{i + 1}}}{h} - a_{i - 1/2}^{n} \frac{{u_m^{i + 1} -
u_{m - 1}^{i + 1}}}{h}}\right)}\right. + \\
+ \left. {\left({a_{i + 1/2}^{n} \frac{{u_{m + 1}^{n} - u_m^{n}}}{h} - a_{n - 1/2}^{n}
\frac{{u_m^{n} {- } u_{m - 1}^{n}}}{h}}\right)}\right] = f(u_m^{i} ) + f^{\prime}_u (u_m^{i} )(u_m^{i + 1} - u_m^{i} ).
\end{gather*}](/sites/default/files/tex_cache/55e85397fe41a15f5f912af20c7f63b2.png)
Здесь также была применена линеаризация функции f(u).
Отдельно рассмотрим важный частный случай a = uk. В довольно грубом приближении уравнение описывает тепловые волны, образующиеся в высокотемпературной плазме и при образовании сверхновых звезд.

Начальное условие для этой задачи u(x, 0) = 0, граничные условия —

Будем искать автомодельное решение задачи, т.е. решение, зависящее не от двух переменных t и x, а от одной, являющейся их комбинацией:

Часто под автомодельными понимают решения, зависящие от безразмерных комбинаций независимых переменных. Введенную переменную иногда называют переменной бегущей волны. В этом случае

тогда рассматриваемое уравнение приобретает вид
- Du' = (uk u')'.
Штрихом здесь обозначено дифференцирование по новой переменной 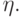 Скорость распространения волны, обозначенная здесь через D, будет определена ниже. После интегрирования обыкновенного
дифференциального уравнения получим
Скорость распространения волны, обозначенная здесь через D, будет определена ниже. После интегрирования обыкновенного
дифференциального уравнения получим

Постоянную интегрирования полагаем равной нулю, так как должно выполняться условие непрерывности теплового потока на фронте тепловой волны. Далее

или  , откуда
, откуда  или
или ![u(\eta ) = \sqrt[k]{{kD}} \cdot (- \eta )^{1/k}](/sites/default/files/tex_cache/88802d34c424a032ab57c29275227702.png) .
.
Интересуют только положительные решения при  , т.е. при
, т.е. при  . При
. При  положим
положим  . В таком случае обобщенное решение (так как в точке
. В таком случае обобщенное решение (так как в точке  получается разрыв первой производной) рассматриваемой задачи будет иметь
вид
получается разрыв первой производной) рассматриваемой задачи будет иметь
вид
![u(\eta ) = \left\{ \begin{array}{cc}
\sqrt[k]{kD(- \eta ) }, & \eta < 0 \\
0, & \eta > 0. \\
\end{array} \right.](/sites/default/files/tex_cache/3a82b02fc65371f8282bd03e4e14b2e4.png)
Скорость фронта тепловой волны легко определяется из граничного условия:

Квазилинейное уравнение вида

имеет качественно различные решения при разных параметрах k и l. Но в окрестности теплового фронта при распространении тепла по нулевому фону все эти решения имеют одинаковую асимптотику, решения в окрестности фронта устроены так же, как и у рассмотренной выше задачи о распространении тепловой волны.




