Численные методы решения уравнений в частных производных
[+]
Опубликован: 25.10.2007 | Доступ: свободный | Студентов: 1276 / 290 | Оценка: 4.40 / 4.36 | Длительность: 21:57:00
Темы: Алгоритмы и дискретные структуры, Математика
Специальности: Математик
Теги: beta, алгоритмы, вторая производная, вычисления, диффузия, задача Коши, законы, искусственная жизнь, исследования, моделирование, невязка, обыкновенное дифференциальное уравнение, однородное уравнение, параллельные вычисления, потоки, собственный вектор, уравнения газовой динамики, уравнениями в частных производных, численное решение уравнений, элементы

Лекция 2: Численное решение дифференциальных уравнений в частных производных параболического типа на примере уравнения теплопроводности

A
|
версия для печати
< Лекция 1 || Лекция 2: 12345678 || Лекция 3 >

Произведя аппроксимацию первого и второго слагаемого в правой части (в невязке) рассматриваемого равенства и учитывая следствия исходного уравнения теплопроводности

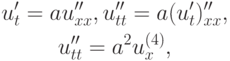
\begin{gather*} u^{\prime}_t = au^{\prime\prime}_{xx}, u^{\prime\prime}_{tt} = a(u^{\prime}_t )^{\prime\prime}_{xx}, \\ u^{\prime\prime}_{tt} = a^2 u_x^{(4)}, \end{gather*}

получим новую схему повышенного порядка точности:

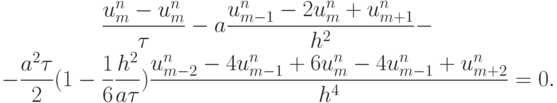
\begin{gather*}\frac{{u_m^{n} - u_m^{n}}}{\tau} - a \frac{{u_{m - 1}^{n} - 2u_m^{n} + u_{m + 1}^{n}}}{{h^2}} - \\ - \frac{{a^2{\tau}}}{2}(1 - \frac{1}{6} \frac{{h^2}}{{a{\tau}}}) \frac{{u_{m - 2}^{n} - 4u_{m - 1}^{n} + 6u_m^{n} - 4u_{m - 1}^{n} + u_{m + 2}^{n}}}{{h^4 }} = 0. \end{gather*}

Трехслойная параметрическая схема для численного решения одномерного линейного уравнения теплопроводности имеет вид

\begin{gather*} \frac{{(1 - \eta )(u_m^{n + 1} - u_m^{n} )}}{\tau} - \eta \frac{{u_m^{n} - u_m^{n - 1}}} {\tau} - \\ - a \left[{(1 - \xi ) \frac{{u_{m - 1}^{n} - 2u_m^{n} + u_{m + 1}^{n}}}{{h^2}} + \xi \frac{{u_{m - 1}^{n + 1} - 2u_m^{n + 1} + u_{m + 1}^{n + 1}}}{{h^2}}}\right] = 0; \end{gather*}

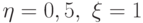при \eta = 0, 5,\ \xi = 1 ее порядок аппроксимации равен O(\tau ^{2}, h^{2}). Недостатком схемы является трехслойность и, следовательно, необходимость ставить дополнительное условие на u't(0, x) .

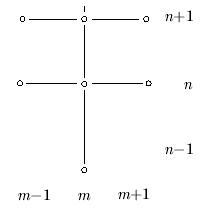
Соответствующий шаблон имеет вид


Рис. 2.1.

В случае если коэффициент теплопроводности a зависит от времени и координат, консервативную схему можно получить, используя интегро - интерполяционный метод (положим, для простоты f(t, x) = 0) . Напомним, что разностная схема называется консервативной, если выполняются следующие условия. В дифференциальной задаче выполняется некий закон сохранения. Соответствующий закон сохранения выполняется и на сеточном уровне. Если же в дифференциальной задаче имеется несколько законов сохранения, а при переходе к сеточному описанию все они получаются как следствие нашей разностной схемы в результате алгебраических преобразований, то схема называется полностью консервативной.

Как правило, при записи уравнений в частных производных законам сохранения соответствует дивергентная форма записи. Для уравнения теплопроводности роль такого закона сохранения играет непрерывность теплового потока.


Рис. 2.2.

Для этого запишем уравнение в дивергентной форме:

\begin{gather*} \frac{{\partial}u}{{\partial}t} + \frac{{\partial}W}{{\partial}x} = 0, \quad \mbox{где} \quad W = - a(t, x) \frac{{\partial}u}{{\partial}x} \mbox{ - тепловой поток, } \\ \mbox{или} \int\limits_{S}(\frac{{\partial}u}{{\partial}t} + \frac{{\partial}W}{{\partial}t}) {dtdx} = \oint\limits_{\Gamma} udx - {Wdt} = 0. \end{gather*}

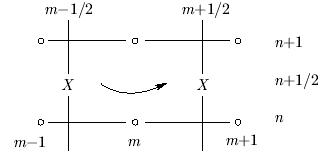
Произведем аппроксимацию последнего интеграла по прямоугольному контуру с узловыми точками (n, m - 1/2), (n, m + 1/2), (n + 1, m + 1/2), (n + 1, m - 1/2 ):

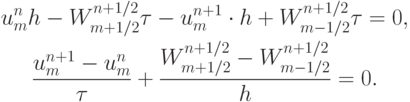
\begin{gather*} u_m^{n} h - W_{m + 1/2}^{n + 1/2}{\tau}- u_m^{n + 1} \cdot h + W_{m - 1/2}^{n + 1/2}{\tau} = 0, \\ \frac{{u_m^{n + 1} - u_m^{n}}}{\tau} + \frac{{W_{m + 1/2}^{n + 1/2} - W_{m - 1/2}^{n + 1/2}}}{h} = 0. \end{gather*}

Отсюда, учитывая вид W_{m \pm 1/2}^{n + 1/2} :

\begin{gather*} W_{m + 1/2}^{n + 1/2} = \frac{1}{2} \left({{a}_{m + 1/2}^{n} \frac{{u_{m + 1}^{n} - u_m^{n}}}{h} + a_{m + 1/2}^{n + 1} \frac{{u_{m + 1}^{n + 1} - u_m^{n + 1}}}{h}}\right), \\ W_{m - 1/2}^{n + 1/2} = \frac{1}{2} \left({a_{m - 1/2}^{n} \frac{{u_m^{n} - u_{m - 1}^{n}}}{h} + a_{m - 1/2}^{n + 1} \frac{{u_m^{n + 1} - u_{m - 1}^{n + 1}}}{h}}\right), \\ \frac{{u_m^{n + 1} - u_m^{n}}}{\tau} + \frac{1}{{2h}} \left[{\left({a_{m + 1/2}^{n} \frac{{u_{m + 1}^{n} - u_m^{n}}}{h} - a_{m - 1/2}^{n} \frac{{u_m^{n} - u_{m - 1}^n }}{h}}\right) + }\right. \\ \left. {+ \left({a_{m + 1/2}^{n + 1} \frac{{u_{m + 1}^{n + 1} - u_m^{n + 1}}}{h} - a_{m - 1/2}^{n + 1} \frac{{u_m^{n + 1} - u_{m - 1}^{n + 1}}}{h}}\right)}\right] = 0 \end{gather*}
Дальше >>
< Лекция 1 || Лекция 2: 12345678 || Лекция 3 >

Вопросы и ответы

вопросов: 0