|
Не могу найти требования по оформлению выпускной контрольной работы по курсу профессиональной переподготовки "Менеджмент предприятия" |
Стратегия и тактика фирмы в отношении спроса
Оценка параметров функции спроса
Для того чтобы планировать свои действия в долгосрочном периоде, фирме необходимо знать типы зависимостей, которыми характеризуется рынок, вплоть до их точной количественной интерпретации. Поэтому зачастую фирме не только приходится собирать нужную информацию относительно взаимосвязи цены и количества продаваемого на рынке товара, но и подбирать теоретическую модель, которая в наибольшей степени соответствовала бы текущей ситуации, а также оценивать параметры модели с точки зрения их достоверности. Рассмотрим, каким образом это происходит.
Первый этап заключается в том, чтобы на основе произведенных наблюдений цены и объема сбыта выбрать подходящую форму предполагаемой зависимости.
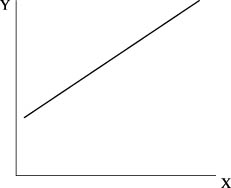
Для спроса могут быть следующие функции:
-
Линейнаягде а0 > 0 ; а1 < 0 - параметры функции спроса; е - показатель случайной ошибки.

-
Логарифмическая

-
Полулогарифмическая

Для анализа издержек (или функции предложения конкурентов) чаще всего используются зависимости:
-
Линейная
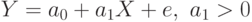
-
Параболическая

-
Логарифмическая
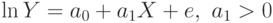
Мы исследуем простую форму взаимосвязи, которая дает общее представление о механизме анализа рынка, поскольку именно простая регрессионная модель является основой для более сложных построений.
Общий вид модели таков:
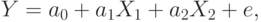
При определении параметров взаимосвязи задача заключается в том, чтобы минимизировать расхождения между реальными данными наблюдений и теоретической моделью. Поскольку отклонения могут быть в обе стороны: как превышение, так и недостижение теоретически вычисленного значения, - целесообразно минимизировать не абсолютные значения отклонений, а их квадраты. Поэтому данный метод получил еще название "метод наименьших квадратов". Использование метода наименьших квадратов предполагает применение обычных математических методов оптимизации, поиски минимального значения какой-либо функции: 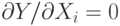 .
.
Второй этап представляет собой оценку значимости параметров. Другими словами, необходимо выяснить, действительно ли (и насколько) мы можем доверять полученной теоретической модели для предсказания будущего поведения рынка.
Предварительное замечание: оценка параметров регрессии базируется на предпосылке о нормальности распределения данных; кроме того, предполагается, что и случайная ошибка имеет нормальное распределение.
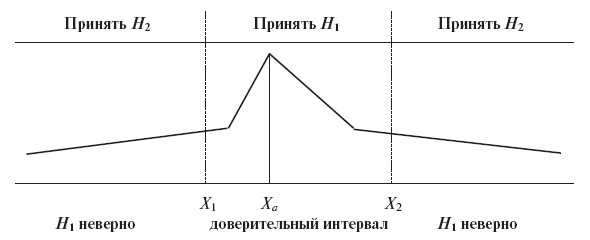
Рис. 6.6. Нормальное распределение, используемое для оценки степени достоверности параметров модели спроса
Методы оценки базируются на проверки двух гипотез: Н1 - гипотеза о наличии зависимости данного рода; Н2 - нулевая гипотеза об отсутствии такой зависимости, a характеризует выбранную точность исследования (вероятность ошибки), Ха является средней показателя, Х1 и Х2 характеризуют доверительный интервал, размер которого задается через выбор a, так что с помощью статистической таблицы можно определить для данного доверительного интервала значение показателя для сравнения с модельным (рис. 6.6).
Два метода: R2 и F, характеризуют регрессию в целом; другие два: стандартная ошибка и t-статистика, применимы для оценки каждого параметры в отдельности. Показатель вероятности используется для оценки как регрессии в целом, так и отдельных параметров.
-
R2
R2 показывает, насколько данная переменная объясняется регрессией, то есть данный показатель можно охарактеризовать как R2 = изменение, объясняемое регрессией / совокупное изменение переменной. R2 измеряется в долях или в процентах. Например, R2 = 0,80 означает, что 80% изменения Y (величины спроса) объясняется изменениями в X (цене товара).
Для простой регрессии показатель рассчитывается как
где Yi - реальное значение объясняемой величины; Yi(T) - ее теоретическое значение (по модели); Ya - среднее значение объясняемой величины.![R^2 = 1 - \left[ {S(Yi - Yi(T))^2 /S(Yi - Ya)^2 } \right],](/sites/default/files/tex_cache/9add2ed99cc3765b20c9ef7de35ceaa7.png)
Чем ближе показатель к единице, тем в большей степени теоретическая модель подходит для наблюдаемых данных. Чем ближе показатель к нулю, тем хуже данная теоретическая модель объясняет реальную зависимость между переменными.
-
Коэффициент F
Коэффициент F показывает, может ли статистически значимая доля совокупного изменения Y быть объяснена через независимые переменные. Рассчитывается по формуле (для простого случая)
где N - число переменных модели; K - число независимых переменных.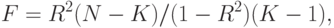
F характеризует степень доверия к модели в случае множественной регрессии (то есть для ситуации, когда объем спроса зависит от нескольких переменных - цены данного товара, цен других товаров, дохода).
Решение принимается на основе сопоставления расчетного (для модели) значения F (FT) с табличным значением F (F*).
Если FT > F*, то нулевую гипотезу о том, что взаимосвязи между переменными не существует, следует отвергнуть, то есть хотя бы один из параметров объясняющих переменных действительно отличен от нуля и может объяснить существующую зависимость. Если же FT < F*, то это означает, что модель не может объяснить существующие зависимости, нулевую гипотезу отвергнуть нельзя.
-
стандартная ошибка
Стандартная ошибка характеризует типичное отклонение реальной величины показателя от его вычисленного значения. стандартная ошибка параметра, как правило, указывается в скобках уравнения регрессии и рассчитывается в компьютерных программах одновременно со значениями параметров. Она нужна для определения доверительного интервала - интервала, где с выбранной вероятностью находятся реальные значения измеряемой величины. Действительное значение величины будет определяться как
где Yi - действительное значение величины; Yi(T) - теоретическое значение величины; s - стандартная ошибка.
Здесь можно применить такое правило: если доверительный интервал (то есть интервал [Yi(T) - 2s; Yi(T) + 2s] ) содержит нуль, то параметр является статистически незначимым (он незначительно отличается от нуля). Если нуля нет, параметру можно доверять.
-
t-статистика
t-статистика проверяет, влияет ли данная независимая переменная на зависимую переменную. Если параметр равен нулю (нулевая гипотеза верна), то при выбранной вероятности оценки t-статистика должна попасть в доверительный интервал распределения t-статисти-ки, который определяется по статистической таблице. Если t-статистика не попадает в данный интервал, то параметр отличен от нуля (нулевая гипотеза неверна). Другими словами, если абсолютное значение t-статистики модели больше t-статистики таблицы (согласно статистическому распределению), то нулевую гипотезу можно отвергнуть. И наоборот.
Значение t-статистики для параметра определяем как
где
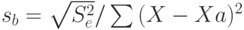 - стандартное отклонение параметра b;
- стандартное отклонение параметра b; 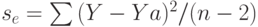 - стандартное отклонение случайного фактора; Xa и Ya - средние значения переменных; X и Y - данные наблюдений; (n - к - 1) степеней свободы модели, n - число переменных модели; k - число независимых переменных.
- стандартное отклонение случайного фактора; Xa и Ya - средние значения переменных; X и Y - данные наблюдений; (n - к - 1) степеней свободы модели, n - число переменных модели; k - число независимых переменных.
Итак, алгоритм проверки значимости параметров состоит из следующих шагов:
- выбрать уровень значимости (вероятность оценки) исследования;
- вычислить t-статистику (часто в компьютерных программах дается одновременно со значением параметра);
- найти табличное значение t-статистики для данного уровня значимости с данными степенями свободы;
- принять решение:
- если t0 > t1 (для положительных параметров)
- или t0 < (-t1) (для отрицательных параметров),
В практических целях при большой выборке ( n > 30 ) часто можно брать за табличное значение t-статистики 2, то есть если |t0| > 2, то нулевую гипотезу можно отвергнуть.
-
Вероятность, при которой нулевая гипотеза неверна.
Данная вероятность характеризует степень объяснимости модели, то есть показывает уровень значимости, при котором нулевая гипотеза верна (а параметры статистически незначимы).
Она рассчитывается по табличным значениям
где P - достигнутый уровень значимости модельных параметров; Рr - вероятность.![P = \Pr \left[ {\left| {t_0 } \right| > t_1 } \right],](/sites/default/files/tex_cache/c7ebc64c979d0dbd5837aeb1342c2bec.png)
Тогда новое правило принятия решения будет таким: если Р нас удовлетворяет ( Р < А, где А - минимальный уровень значимости, подходящий для модели, выбирается заранее), то нулевую гипотезу можно отвергнуть.