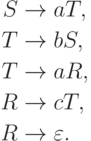НОУ ИНТУИТ | Математическая теория формальных языков. Лекция 4: Основные свойства автоматных языков

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Московский государственный университет имени М.В.Ломоносова

Опубликован: 09.07.2007 | Доступ: свободный | Студентов: 2513 / 1034 | Оценка: 4.56 / 4.26 | Длительность: 20:40:00

ISBN: 978-5-9556-0062-8

Темы: Программирование, Алгоритмы и дискретные структуры, Математика

Специальности: Математик

Теги: beta, finite, grammar, xml, автоматы, анализ, булева формула, дерево вывода, контекстно-свободная грамматика, контекстно-свободный язык, метка перехода, моноид, нетерминальный символ, протоколы, регулярные выражения, теория, шаг индукции, элементы

|

Вам нравится? Нравится 33 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Аннотация: В данной лекции доказываются свойства замкнутости класса всех автоматных языков относительно итерации, конкатенации, объединения, дополнения и пересечения, доказывается так называемая лемма о разрастании, которая во многих случаях позволяет установить неавтоматность формального языка. Приведены практические примеры и предоставлены упражнения для самостоятельного решения

Ключевые слова: формальный язык, lemma, Законы де Моргана

Для практического применения теории конечных автоматов нужны средства, позволяющие выяснять, является ли некоторый формальный язык автоматным. Для получения положительного ответа на такой вопрос могут пригодиться достаточные условия автоматности, для отрицательного ответа - необходимые условия автоматности. В этой лекции рассматриваются наиболее часто используемые условия, касающиеся автоматности формального языка.

В первых двух разделах этой лекции доказываются свойства замкнутости класса всех автоматных языков (относительно итерации, конкатенации, объединения, дополнения, пересечения и т. д.). Эти свойства можно использовать как достаточные условия автоматности. Например, если нужно выяснить, является ли язык L автоматным, и удается представить L в виде 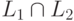$L_1 \cap L_2$ , где языки L₁ и L₂ автоматные, то и язык L обязательно является автоматным.

В последних двух разделах этой лекции доказывается так называемая лемма о разрастании (в англоязычной литературе pumping lemma), которая во многих случаях позволяет установить неавтоматность формального языка. К сожалению, эта лемма помогает не всегда, так как дает всего лишь необходимое условие, а не критерий автоматности.

3.1. Свойства замкнутости класса автоматных языков

Теорема 3.1.1. Класс автоматных языков замкнут относительно итерации, конкатенации и объединения.

Доказательство. Без ограничения общности можно предположить, что каждый из исходных языков задан конечным автоматом с одним начальным и одним заключительным состоянием. Тогда во всех трех случаях результирующий автомат получается из исходных путем добавления нескольких $\varepsilon$ -переходов и состояний и назначения новых начальных и заключительных состояний.

Пример 3.1.2. Пусть 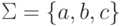$\Sigma = \{ a , b , c \}$ . Рассмотрим конечный автомат

$M_1 = \langle \{ 1 , 2 , 3 \}, \Sigma , \Delta_1 , \{ 1 \} , \{ 2 \} \rangle ,$

где

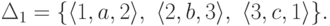
$\Delta_1 = \{ \langle 1 , a , 2 \rangle ,\ \langle 2 , b , 3 \rangle ,\ \langle 3 , c , 1 \rangle \} .$

$\objectwidth={5mm} \objectheight={5mm} \let\objectstyle=\scriptstyle \xymatrix { *=[o][F-]{1} \ar @`{+/l16mm/} [] ^{} \ar "1,2" ^{a} & *=[o][F=]{2} \ar "2,2" ^{b} \\ % & *=[o][F-]{3} \ar "1,1" ^{c} }$

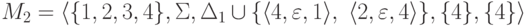Тогда язык L(M₁)^* распознается конечным автоматом $M_2 = \langle \{ 1 , 2 , 3 , 4 \} , \Sigma , \Delta_1 \cup \{ \langle 4 , \varepsilon , 1 \rangle ,\ \langle 2 , \varepsilon , 4 \rangle \} , \{ 4 \} , \{ 4 \} \rangle$ .

$\objectwidth={5mm} \objectheight={5mm} \let\objectstyle=\scriptstyle \xymatrix { *=[o][F=]{4} \ar @`{+/l16mm/} [] ^{} \ar "2,1" _{\varepsilon} & \\ *=[o][F-]{1} \ar "2,2" ^{a} & *=[o][F-]{2} \ar "3,2" ^{b} \ar "1,1" _{\varepsilon} \\ % & *=[o][F-]{3} \ar "2,1" ^{c} }$

Пример 3.1.3. Пусть 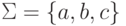$\Sigma \peq \{ a , b , c \}$ . Рассмотрим конечный автомат M₁ из примера 3.1.2 и конечный автомат

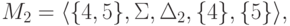
$M_2 = \langle \{ 4 , 5 \} , \Sigma , \Delta_2 , \{ 4 \} , \{ 5 \} \rangle ,$

где

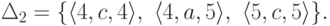
$\Delta_2 = \{ \langle 4 , c , 4 \rangle ,\ \langle 4 , a , 5 \rangle ,\ \langle 5 , c , 5 \rangle \} .$

$\objectwidth={5mm} \objectheight={5mm} \let\objectstyle=\scriptstyle \xymatrix { *=[o][F-]{4} \ar @`{+/l16mm/} [] ^{} \rloop{0,1} ^{c} \ar "1,2" ^{a} & *=[o][F=]{5} \rloop{0,1} ^{c} }$

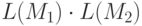Тогда язык $L ( M_1 ) \cdot L ( M_2 )$ распознается конечным автоматом

$M_3 \peq \langle \{ 1 , 2 , 3 , 4 , 5 \} , \Sigma , \Delta_1 {{}\cup{}} \Delta_2 {{}\cup{}} \{ \lp 2 , \emptyword , 4 \rp \} , \{ 1 \} , \{ 5 \} \rangle ,$

$\objectwidth={5mm} \objectheight={5mm} \let\objectstyle=\scriptstyle \xymatrix { *=[o][F-]{1} \ar @`{+/l16mm/} [] ^{} \ar "1,2" ^{a} & *=[o][F-]{2} \ar "2,2" ^{b} \ar "1,3" ^{\varepsilon} & *=[o][F-]{4} \rloop{0,1} ^{c} \ar "1,4" ^{a} & *=[o][F=]{5} \rloop{0,1} ^{c} \\ % & *=[o][F-]{3} \ar "1,1" ^{c} & & }$

а язык $L ( M_1 ) \cup L ( M_2 )$ распознается конечным автоматом

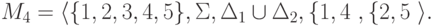
$M_4 = \langle \{ 1 , 2 , 3 , 4 , 5 \} , \Sigma , \Delta_1 \cup \Delta_2 , \{ 1 , 4 \ }, \{ 2 , 5 }\ \rangle .$

$\objectwidth={5mm} \objectheight={5mm} \let\objectstyle=\scriptstyle \xymatrix { *=[o][F-]{4} \ar @`{+/l16mm/} [] ^{} \rloop{0,1} ^{c} \ar "1,2" ^{a} & *=[o][F=]{5} \rloop{0,1} ^{c} \\ *=[o][F-]{1} \ar @`{+/l16mm/} [] ^{} \ar "2,2" ^{a} & *=[o][F=]{2} \ar "3,2" ^{b} \\ % & *=[o][F-]{3} \ar "2,1" ^{c} }$

Упражнение 3.1.4. Существует ли такой автоматный язык L, что язык L^R не является автоматным?

Упражнение 3.1.5. Существует ли такой автоматный язык $L \subseteq \Sigma ^*$ , что язык Pref(L) не является автоматным?

Упражнение 3.1.6. Существует ли такой автоматный язык $L \subseteq \Sigma ^*$ , что язык Suf(L) не является автоматным?

Упражнение 3.1.7. Существует ли такой автоматный язык $L \subseteq \Sigma ^*$ , что язык Subw(L) не является автоматным?

Упражнение 3.1.8. Существует ли такой автоматный язык $L \subseteq \Sigma ^*$ , что язык Subseq(L) не является автоматным?

Упражнение 3.1.9. Существует ли такой автоматный язык L, что язык

$\mathrm{Cycle} ( L ) \rightleftharpoons \{ x y \mid y x \in L \; \text{для некоторых слов} \; x \; \text{и} \; y \}$

не является автоматным?

Упражнение 3.1.10. Существует ли такой автоматный язык L, что язык

$\{ w \mid w \in L \text{ или } w^R \in L \}$

не является автоматным?

Упражнение 3.1.11. Найти праволинейную грамматику, порождающую язык

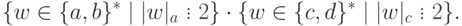
$\{ w \in \{a,b\}^* \mid | w |_a \ \vdots \ 2 \} \cdot \{ w \in \{c,d\}^* \mid | w |_c \ \vdots \ 2 \} .$

Упражнение 3.1.12. Найти праволинейную грамматику, порождающую язык L^*, если язык L порождается грамматикой

$\begin{align*} S \; & {\to} \; a T, \\ T \; & {\to} \; b S, \\ T \; & {\to} \; a R, \\ R \; & {\to} \; c T, \\ R \; & {\to} \; \varepsilon . \end{align*}$

Дальше >>

Авторизоваться

Математическая теория формальных языков

Основные свойства автоматных языков

3.1. Свойства замкнутости класса автоматных языков

Вопросы и ответы