|
Упражнение 2.1.25 |
Регулярные выражения
До сих пор мы рассматривали два способа конечного описания формального языка: грамматики и автоматы. Третий способ, часто наиболее удобный и компактный, - регулярные выражения. В них используются символы, обозначающие итерацию, конкатенацию и объединение языков. Например, для обозначения итерации традиционно используется символ "звездочка".
Регулярные выражения находят практическое применение во многих компьютерных приложениях, таких как текстовые редакторы и интерпретаторы командной строки. В автоматических генераторах лексических анализаторов принято использовать именно регулярные выражения в качестве формализма, с помощью которого задаются классы однотипных лексем (например, класс идентификаторов, класс десятичных констант). В языках программирования Perl, Python и др. имеется встроенная поддержка регулярных выражений.
В начале лекции даются необходимые определения. Затем в разделе 5.2* приводятся некоторые тождества регулярных выражений, такие как ассоциативность конкатенации, дистрибутивность конкатенации относительно объединения и др. В разделе 5.3 доказывается, что регулярные выражения задают в точности класс автоматных языков. В разделе 5.4* формулируется теорема о классификации автоматных языков по их сложности, измеряемой звездной высотой (необходимой глубиной вложенности итераций при задании данного языка регулярным выражением).
5.1. Определение регулярного выражения
Определение 5.1.1. Регулярное выражение
над алфавитом  определяется рекурсивно следующим образом: 0 является регулярным выражением; 1 является регулярным выражением;
если
определяется рекурсивно следующим образом: 0 является регулярным выражением; 1 является регулярным выражением;
если 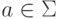 , то a является
регулярным выражением;
если e и f являются регулярными выражениями, то
, то a является
регулярным выражением;
если e и f являются регулярными выражениями, то  ,
,  и
и  тоже являются регулярными выражениями.
тоже являются регулярными выражениями.
Для экономии скобок будем считать, что
операция *
связывает сильнее
(то есть имеет более высокий приоритет), чем умножение,
а умножение связывает сильнее, чем сложение.
Вместо  часто пишут просто
часто пишут просто  .
.
Пример 5.1.2.
Пусть  .
Тогда
.
Тогда 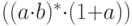 является регулярным выражением над алфавитом
является регулярным выражением над алфавитом  .
.
Определение 5.1.3.
Каждое регулярное выражение e
над алфавитом  задает
(denotes, represents)
некоторый язык над алфавитом
задает
(denotes, represents)
некоторый язык над алфавитом  (обозначение
(обозначение  ),
определяемое рекурсивно следующим образом:
),
определяемое рекурсивно следующим образом:

Вместо  часто пишут просто e.
часто пишут просто e.
Пример 5.1.4.
Пусть  .
Согласно определению
.
Согласно определению

Определение 5.1.5. Язык L называется регулярным если он задается некоторым регулярным выражением.
Определение 5.1.6.
Пусть e -
регулярное выражение.
Тогда  .
.
Упражнение 5.1.7. Упростить регулярное выражение ((a+bc)*)*
Упражнение 5.1.8. Найти праволинейную грамматику для языка ab*a
Упражнение 5.1.9. Найти праволинейную грамматику для языка ((a+b)a)*.
Упражнение 5.1.10. Найти полный детерминированный конечный автомат для языка (a+b)*(aab+abaa+abb)(a+b)*.
Упражнение 5.1.11. Найти полный детерминированный конечный автомат для языка (a+b)*(a(b+1)abb+baa)(a+b)*.
Упражнение 5.1.12. Найти полный детерминированный конечный автомат для языка (b+c)((ab)*c+(ba)*)*.
Упражнение 5.1.13. Найти полный детерминированный конечный автомат для языка (abab)+(aba)*.
Упражнение 5.1.14. Найти полный детерминированный конечный автомат для языка (c+(a+b+c)(b+a(b+c)*a))*(a+b+c).
5.2*. Свойства регулярных выражений
Лемма 5.2.1. Регулярные выражения образуют ассоциативное полукольцо с операциями 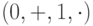 , то есть для любых регулярных выражений e, f
и g выполняются следующие тождества:
, то есть для любых регулярных выражений e, f
и g выполняются следующие тождества:
- e+f = f+e ;
- e+0 = e ;
-
 ;
; -
 ;
; -
 ;
; -
 ;
; -
 ;
; -
 ;
; -
 ;
; -
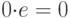 .
.
Равенство понимается как равенство языков, задаваемых регулярными выражениями.
Лемма 5.2.2. Для любых регулярных выражений e и f выполняются следующие тождества:
- e+e = e ;
-
(1+e+ee+...+en-1)(en)* = e*
для любого
 ;
; - (e*f)*e* = (e+f)* ;
- 1+e(fe)*f = (ef)*.
Лемма 5.2.3. Для любых регулярных выражений e, f и g, если e = ef+g
и 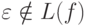 ,
то e = gf*.
,
то e = gf*.
Упражнение 5.2.4. Упростить регулярное выражение 0*.
Упражнение 5.2.5. Упростить регулярное выражение (a+b+ab)*.
Упражнение 5.2.6. Упростить регулярное выражение (a*b)*+(b*a)*.
Упражнение 5.2.7. Упростить регулярное выражение ((b+a)*b+1)b*.
Упражнение 5.2.8. Упростить регулярное выражение ((ab+aab)*a*)*.
Упражнение 5.2.9. Упростить регулярное выражение (abbaab+abbaaba)*.
Упражнение 5.2.10. Упростить регулярное выражение (a+b)*(a(a+b)*a+b(a+b)*b).
Упражнение 5.2.11. Упростить регулярное выражение (eb*(1+c(d+ab*c)*a)b*f)*eb*c(d+ab*c)*.
