НОУ ИНТУИТ | Математическая теория формальных языков. Лекция 13: Детерминированные контекстно-свободные языки

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Московский государственный университет имени М.В.Ломоносова

Опубликован: 09.07.2007 | Доступ: свободный | Студентов: 2513 / 1034 | Оценка: 4.56 / 4.26 | Длительность: 20:40:00

ISBN: 978-5-9556-0062-8

Темы: Программирование, Алгоритмы и дискретные структуры, Математика

Специальности: Математик

Теги: beta, finite, grammar, xml, автоматы, анализ, булева формула, дерево вывода, контекстно-свободная грамматика, контекстно-свободный язык, метка перехода, моноид, нетерминальный символ, протоколы, регулярные выражения, теория, шаг индукции, элементы

|

Вам нравится? Нравится 33 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Аннотация: В данной лекции рассматриваются детерминированные контекстно-свободные языки. Формулируется ряд свойств этого класса языков, рассматривается важность детерминированных контекстно-свободных языков для теоретической информатики, которая заключается в том, что для каждого такого языка можно указать быстрый алгоритм, распознающий принадлежность слова этому языку. Приведены практические примеры и упражнения для самостоятельного решения

Ключевые слова: класс, специальный символ, алгоритм, deterministic, контекстно-свободный язык, шаг индукции, контекстно-свободная грамматика

К сожалению, теорема о детерминизации не переносится с конечных автоматов на автоматы с магазинной памятью. Возникает важный для практических приложений класс языков, распознаваемых детерминированными автоматами с магазинной памятью (то есть такими автоматами с магазинной памятью, которые ни в какой конфигурации не могут выбирать между несколькими очередными тактами). Точные определения этого класса автоматов и соответствующего класса языков даны в разделе 12.1. Чтобы получить полезный и естественный с точки зрения практики класс, нужно добавить в конец каждого слова специальный символ, называемый маркером конца слова. Языки из выделенного таким образом класса называются детерминированными контекстно-свободными языками. Во втором разделе лекции формулируется ряд свойств этого класса языков. Важность детерминированных контекстно-свободных языков для теоретической информатики обусловлена тем, что для каждого такого языка можно указать быстрый алгоритм, распознающий принадлежность слова этому языку.

12.1. Детерминированные автоматы с магазинной памятью

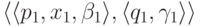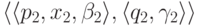Определение 12.1.1. Будем говорить, что два перехода МП-автомата $\lp \lp p_1 , x_1 , \beta_1 \rp , \lp q_1 , \gamma_1 \rp \rp$ и $\lp \lp p_2 , x_2 , \beta_2 \rp , \lp q_2 , \gamma_2 \rp \rp$ являются совместными, если

p₁ = p₂ ;
$x_1 \prefix x_2$ или $x_2 \prefix x_1$ ;
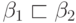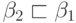$\beta_1 \prefix \beta_2$ или $\beta_2 \prefix \beta_1$ .

Определение 12.1.2. МП-автомат называется детерминированным (deterministic), если он имеет ровно одно начальное состояние и все переходы этого автомата попарно несовместны.

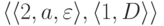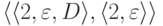Пример 12.1.3. МП-автомат M из примера 10.2.8 не является детерминированным, так как переходы $\lp \lp 2 , a , \varepsilon \rp , \lp 1 , D \rp \rp$ и $\lp \lp 2 , \varepsilon , D \rp , \lp 2 , \varepsilon \rp \rp$ совместны.

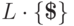Определение 12.1.4. Язык L над алфавитом $\Sigma$ называется детерминированным контекстно-свободным языком, если существует детерминированный МП-автомат, распознающий язык $L \cdot \{ \eos \}$ над алфавитом 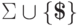$\Sigma \cup \{ \eos \}$ , где $\eos$ - дополнительный символ, не принадлежащий множеству $\Sigma$ . Символ $\eos$ называется маркером конца строки.

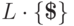Пример 12.1.5. Рассмотрим алфавит $\Sigma = \{ a , b \}$ . Язык $L \peq \{ a^m b^n \mid m = n \rusor n = 0 \}$ - детерминированный контекстно-свободный язык, так как язык $L \cdot \{ \eos \}$ порождается детерминированным МП-автоматом (хотя язык L не порождается никаким детерминированным МП-автоматом).

Пример 12.1.6. Язык L, распознаваемый МП-автоматом M из примера 10.2.8, является детерминированным контекстно-свободным языком, так как язык 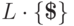$L \cdot \{ \eos \}$ порождается детерминированным МП-автоматом

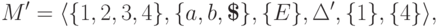
$M' = \lalg \{ 1 , 2 , 3 , 4 \} , \{ a , b , \eos \} , \{ E \} , \Delta' , \{ 1 \} , \{ 4 \} \ralg ,$

где

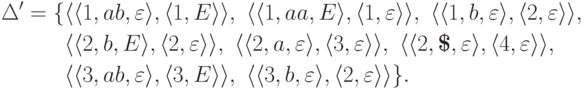
$\begin{align*} \Delta' &= \{ \lp \lp 1 , ab , \varepsilon \rp , \lp 1 , E \rp \rp ,\ \lp \lp 1 , aa , E \rp , \lp 1 , \varepsilon \rp \rp ,\ \lp \lp 1 , b , \varepsilon \rp , \lp 2 , \varepsilon \rp \rp ,\ \\ &\hphantom{ {} = {} \{ } %\} \lp \lp 2 , b , E \rp , \lp 2 , \varepsilon \rp \rp ,\ \lp \lp 2 , a , \varepsilon \rp , \lp 3 , \varepsilon \rp \rp ,\ \lp \lp 2 , \eos , \varepsilon \rp , \lp 4 , \varepsilon \rp \rp ,\ \\ &\hphantom{ {} = {} \{ } %\} \lp \lp 3 , ab , \varepsilon \rp , \lp 3 , E \rp \rp ,\ \lp \lp 3 , b , \varepsilon \rp , \lp 2 , \varepsilon \rp \rp \} . \end{align*}$

$\objectwidth={5mm} \objectheight={5mm} \let\objectstyle=\scriptstyle \xymatrix @=11mm{ % & *=[o][F-]{3} \rloop{0,1} ^{ab,\varepsilon:E} \ar "2,2" <1.0mm> ^{b,\varepsilon:\varepsilon} & \\ *=[o][F-]{1} \ar @`{+/l16mm/} [] ^{} \rloop{0,1} ^{ab,\varepsilon:E} \rloop{0,-1} ^{aa,E:\varepsilon} \ar "2,2" ^{b,\varepsilon:\varepsilon} & *=[o][F-]{2} \rloop{0,-1} ^{b,E:\varepsilon} \ar "1,2" <1.0mm> ^{a,\varepsilon:\varepsilon} \ar "2,3" ^{\boldsymbol{\$},\varepsilon:\varepsilon} & *=[o][F=]{4} }$

Упражнение 12.1.7. Является ли детерминированным контекстно-свободный язык 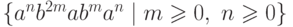$\{ a^n b^{2m} a b^m a^n \mid m \geq 0 ,\ n \geq 0 \}$ ?

Дальше >>

Авторизоваться

Математическая теория формальных языков

Детерминированные контекстно-свободные языки

12.1. Детерминированные автоматы с магазинной памятью

Вопросы и ответы