|
Упражнение 2.1.25 |
Дополнительные свойства контекстно-свободных языков
В этой лекции излагаются те свойства контекстно-свободных языков, которые удобно доказывать с привлечением автоматов с магазинной памятью. В первых двух разделах приводятся некоторые свойства замкнутости класса контекстно-свободных языков (замкнутость относительно деления, взятия гомоморфного образа и полного гомоморфного прообраза). В конце лекции формулируются два критерия контекстной свободности, интересных в основном с теоретической точки зрения.
11.1*. Деление контекстно-свободных языков
Теорема 11.1.1. Пусть L1 - контекстно-свободный язык
над алфавитом  и L2 - автоматный язык над алфавитом
и L2 - автоматный язык над алфавитом  . Тогда язык
. Тогда язык  является контекстно-свободным.
является контекстно-свободным.
Доказательство.
Пусть 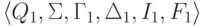 -
МП-автомат,
распознающий язык L1.
Без ограничения общности можно считать, что
для каждого перехода
-
МП-автомат,
распознающий язык L1.
Без ограничения общности можно считать, что
для каждого перехода 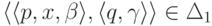 выполняется неравенство
выполняется неравенство  .
.
Пусть  -
конечный автомат,
распознающий язык L2.
Без ограничения общности можно считать, что
-
конечный автомат,
распознающий язык L2.
Без ограничения общности можно считать, что

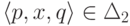 выполняется равенство |x| = 1.
выполняется равенство |x| = 1.Тогда язык 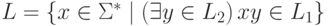 распознается МП-автоматом
распознается МП-автоматом 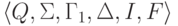 ,
где
,
где 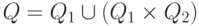 , I = I1,
, I = I1, 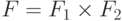 и
и
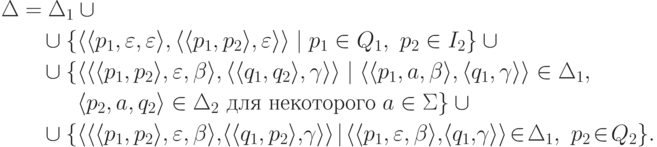
Пример 11.1.2.
Пусть  ,
язык L1
распознается МП-автоматом
,
язык L1
распознается МП-автоматом
![\objectwidth={5mm} \objectheight={5mm} \let\objectstyle=\scriptstyle
\xymatrix {
*=[o][F-]{1}
\ar @`{+/l16mm/} [] ^{}
\rloop{0,1} ^{a,\varepsilon:C}
\ar "2,1" ^{\varepsilon,\varepsilon:C}
\\
*=[o][F=]{2}
\ar @`{+/l16mm/} [] ^{}
\rloop{0,-1} ^{b,C:\varepsilon}
}](/sites/default/files/tex_cache/52923040a8c408d393477d98d48445cf.png)
![\objectwidth={5mm} \objectheight={5mm} \let\objectstyle=\scriptstyle
\xymatrix {
*=[o][F-]{3}
\ar @`{+/l16mm/} [] ^{}
\ar "1,2" <0.6mm> ^{b}
& *=[o][F=]{4}
\ar "1,1" <0.6mm> ^{b}
}
\ .](/sites/default/files/tex_cache/6714c02c5ab25a6ae602f82ba88c7c1b.png)

![\objectwidth={7.5mm} \objectheight={7.5mm} \let\objectstyle=\scriptstyle
\xymatrix {
*=[o][F-]{1}
\ar @`{+/l16mm/} [] ^{}
\rloop{0,1} ^{a,\varepsilon:C}
\ar "2,1" ^{\varepsilon,\varepsilon:C}
\ar "1,2" ^{\varepsilon,\varepsilon:\varepsilon}
& *=[o][F-]{1,3}
\ar "2,2" ^{\varepsilon,\varepsilon:C}
& *=[o][F-]{1,4}
\ar "2,3" ^{\varepsilon,\varepsilon:C}
\\
*=[o][F-]{2}
\ar @`{+/l16mm/} [] ^{}
\rloop{0,-1} ^{b,C:\varepsilon}
\ar "2,2" ^{\varepsilon,\varepsilon:\varepsilon}
& *=[o][F-]{2,3}
\ar "2,3" <0.6mm> ^{\varepsilon,C:\varepsilon}
& *=[o][F=]{2,4}
\ar "2,2" <0.6mm> ^{\varepsilon,C:\varepsilon}
}](/sites/default/files/tex_cache/1ac37bee282d400b169df34101c56866.png)
Пример 11.1.3.
Пусть  ,
, 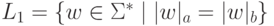 и
и  .
Тогда
.
Тогда
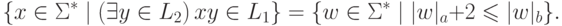
Пример 11.1.4.
Пусть  ,
, 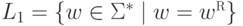 и
и 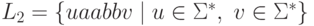 .
Тогда
.
Тогда
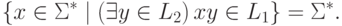
Замечание 11.1.5.
Пусть 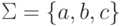 и
и  .
Язык
.
Язык 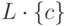 является контекстно-свободным
тогда и только тогда, когда
язык L
является контекстно-свободным.
является контекстно-свободным
тогда и только тогда, когда
язык L
является контекстно-свободным.
Упражнение 11.1.6.
Существует ли такой контекстно-свободный язык  ,
что язык Subw
не является контекстно-свободным?
,
что язык Subw
не является контекстно-свободным?
Упражнение 11.1.7. Существует ли такой
контекстно-свободный язык L
над алфавитом {a,b},
что язык 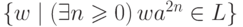 не является контекстно-свободным?
не является контекстно-свободным?
Упражнение 11.1.8. Существует ли такой контекстно-свободный язык L над алфавитом {a,b}, что язык

