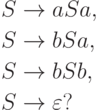|
Упражнение 2.1.25 |
Основные свойства автоматных языков
3.3. Лемма о разрастании для автоматных языков
Лемма 3.3.1 (pumping lemma, лемма о разрастании, лемма о накачке,
лемма-насос). Пусть L автоматный язык над алфавитом  . Тогда найдется такое положительное целое число p, что для любого слова
. Тогда найдется такое положительное целое число p, что для любого слова 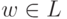 длины не меньше p можно подобрать слова
длины не меньше p можно подобрать слова 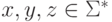 , для которых верно xyz = w,
, для которых верно xyz = w, 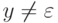 ,
,  и
и 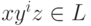 для всех
для всех  .
.
Доказательство.
Пусть язык L
распознается конечным автоматом  ,
содержащим только переходы с метками длины единица.
Положим p = |Q|.
Пусть слово w
является меткой успешного пути
,
содержащим только переходы с метками длины единица.
Положим p = |Q|.
Пусть слово w
является меткой успешного пути
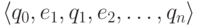
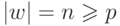 .
Согласно принципу Дирихле найдутся такие индексы j и k,
что
.
Согласно принципу Дирихле найдутся такие индексы j и k,
что  и qj = qk
(ведь множество индексов
и qj = qk
(ведь множество индексов 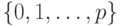 содержит p+1
натуральных чисел,
а значения qi
берутся из множества, содержащего всего p элементов).
Выберем слова x, y и z
так, что |x| = j, |y| = k - j
и xyz = w.
содержит p+1
натуральных чисел,
а значения qi
берутся из множества, содержащего всего p элементов).
Выберем слова x, y и z
так, что |x| = j, |y| = k - j
и xyz = w.Пример 3.3.2.
Пусть  .
Рассмотрим автоматный язык
.
Рассмотрим автоматный язык
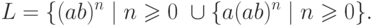
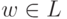 длины не меньше p
найдутся слова
длины не меньше p
найдутся слова 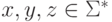 ,
соответствующие утверждению леммы 3.3.1.
Действительно, если w = abu
для некоторого слова u,
то положим
,
соответствующие утверждению леммы 3.3.1.
Действительно, если w = abu
для некоторого слова u,
то положим 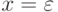 , y = ab, z = u ;
иначе w = aabu
и можно положить x = a, y = ab, z = u.
, y = ab, z = u ;
иначе w = aabu
и можно положить x = a, y = ab, z = u.Упражнение 3.3.3. Является ли автоматным язык
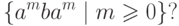
Упражнение 3.3.4. Является ли автоматным язык {an | существует такое число  , что p простое и p + 2 простое} ?
, что p простое и p + 2 простое} ?
Упражнение 3.3.5. Является ли автоматным язык
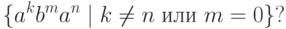
Упражнение 3.3.6. Является ли автоматным язык
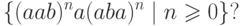
Упражнение 3.3.7. Является ли автоматным язык

Упражнение 3.3.8. Является ли автоматным язык
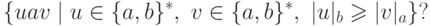
Упражнение 3.3.9. Является ли автоматным язык

Упражнение 3.3.10. Является ли автоматным язык, порождаемый грамматикой