НОУ ИНТУИТ | Математическая теория формальных языков. Лекция 4: Основные свойства автоматных языков

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Московский государственный университет имени М.В.Ломоносова

Опубликован: 09.07.2007 | Доступ: свободный | Студентов: 2513 / 1034 | Оценка: 4.56 / 4.26 | Длительность: 20:40:00

ISBN: 978-5-9556-0062-8

Темы: Программирование, Алгоритмы и дискретные структуры, Математика

Специальности: Математик

Теги: beta, finite, grammar, xml, автоматы, анализ, булева формула, дерево вывода, контекстно-свободная грамматика, контекстно-свободный язык, метка перехода, моноид, нетерминальный символ, протоколы, регулярные выражения, теория, шаг индукции, элементы

|

Вам нравится? Нравится 33 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

3.2. Пересечение и дополнение автоматных языков

Теорема 3.2.1. Класс автоматных языков замкнут относительно дополнения и пересечения.

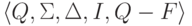Доказательство. Если язык L распознается полным детерминированным конечным автоматом $\langle Q , \Sigma , \Delta , I , F \rangle$ , то язык $\Sigma ^* - L$ распознается конечным автоматом $\langle Q , \Sigma , \Delta , I , Q - F \rangle$ .

Пересечение выражается через объединение и дополнение (закон де Моргана).

Замечание 3.2.2. Автоматность пересечения двух автоматных языков можно легко доказать и без привлечения теоремы 2.7.1. Для этого достаточно построить по двум конечным автоматам с однобуквенными переходами

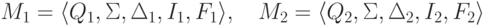
$M_1 = \langle Q_1 , \Sigma , \Delta_1 , I_1 , F_1 \rangle ,\quad M_2 = \langle Q_2 , \Sigma , \Delta_2 , I_2 , F_2 \rangle$

новый конечный автомат

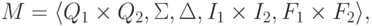
$M = \langle Q_1 \times Q_2 , \Sigma , \Delta , I_1 \times I_2 , F_1 \times F_2 \rangle ,$

где

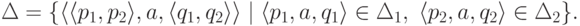
$\Delta = \{ \langle \langle p_1 , p_2 \rangle , a , \langle q_1 , q_2 \rangle \rangle \mid \langle p_1 , a , q_1 \rangle \in \Delta_1, \; \langle p_2 , a , q_2 \rangle \in \Delta_2 \} .$

Упражнение 3.2.3. Обозначим через L язык, порождаемый грамматикой

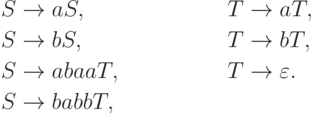
$\begin{align*} S \; & {\to} \; a S , & T \; & {\to} \; a T , \\ S \; & {\to} \; b S , & T \; & {\to} \; b T , \\ S \; & {\to} \; abaa T , & T \; & {\to} \; \varepsilon . \\ S \; & {\to} \; babb T , \end{align*}$

Найти праволинейную грамматику, порождающую язык $\{a,b\}^* - L$ .

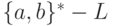Упражнение 3.2.4. Обозначим через L язык, порождаемый грамматикой

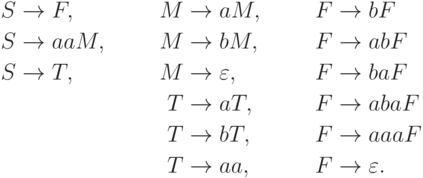
$\begin{align*} S \; & {\to} \; F , & M \; & {\to} \; a M , & F \; & {\to} \; b F \\ S \; & {\to} \; a a M , & M \; & {\to} \; b M , & F \; & {\to} \; ab F \\ S \; & {\to} \; T , & M \; & {\to} \; \varepsilon , & F \; & {\to} \; ba F \\ & & T \; & {\to} \; a T , & F \; & {\to} \; aba F \\ & & T \; & {\to} \; b T , & F \; & {\to} \; aaa F \\ & & T \; & {\to} \; a a , & F \; & {\to} \; \varepsilon . \end{align*}$

Найти праволинейную грамматику, порождающую язык $\{a,b\}^* - L$ .

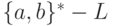Упражнение 3.2.5. Обозначим через L язык, порождаемый грамматикой

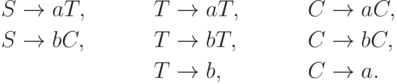
$\begin{align*} S \; & {\to} \; a T , & T \; & {\to} \; a T , & C \; & {\to} \; a C , \\ S \; & {\to} \; b C , & T \; & {\to} \; b T , & C \; & {\to} \; b C , \\ & & T \; & {\to} \; b , & C \; & {\to} \; a . \end{align*}$

Найти праволинейную грамматику, порождающую язык $\{a,b\}^* - L$ .

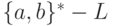Упражнение 3.2.6. Существуют ли такие детерминированные конечные автоматы M₁ и M₂, что язык $L(M_1) \cup L(M_2)$ не порождается ни одним детерминированным конечным автоматом с количеством состояний n₁n₂+n₁+n₂, где n₁ - количество состояний автомата M₁ и n₂ - количество состояний автомата M₂?

Дальше >>

Авторизоваться

Математическая теория формальных языков

Основные свойства автоматных языков

3.2. Пересечение и дополнение автоматных языков

Вопросы и ответы