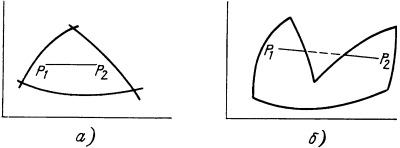Введение в математическое программирование
[+]
Донецкий национальный технический университет
Опубликован: 09.07.2007 | Доступ: свободный | Студентов: 3129 / 724 | Оценка: 4.34 / 4.12 | Длительность: 13:54:00
Темы: Алгоритмы и дискретные структуры, Математика
Специальности: Программист
Теги: beta, анализ, базисное решение, вычисления, двойственная задача, задача линейного программирования, законы, искусственная жизнь, исследования, метод полного исключения, моделирование, нелинейное программирование, оптимальный план, поиск, программирование, симплекс, симплекс-метод, функция лагранжа, экстремум функции, электронная почта, элементы

Лекция 12: Оптимизация при наличии ограничений. Ограничения в виде равенств. Ограничения в виде неравенств. Выпуклость и вогнутость. Комплексный метод

A
|
версия для печати
< Лекция 11 || Лекция 12: 1234 || Лекция 13 >

3. Выпуклость и вогнутость

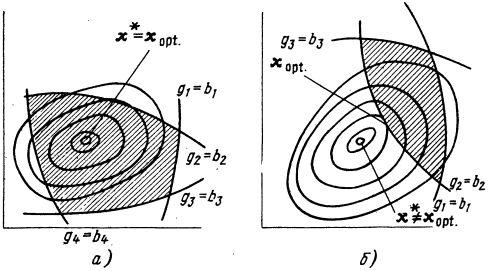
Общая задача математического программирования является очень сложной и до cих пор не имеет полного решения. Некоторые трудности встречаются в задачах, графически проиллюстрированных (рис. 12.1). На рисунке изображены линии постоянного уровня функции. По мере перемещения от точки х* - точки минимума функции при отсутствии ограничений - значения функции будут расти. На рис. 12.1 показаны также границы области ограничений gi(x) = bi, а сама область заштрихована.

На рис. 12.1,a минимум функции при наличии ограничений совпадает с минимумом функции без ограничений. Все ограничения имеют вид строгих неравенств, и, зная это, можно было бы пренебречь ограничениями и решить зaдачу методами, изложенными в изложенными ранее. На рис. 12.1,б точка минимума при наличии ограничений лежит на кривой g2(x) = b2, а два других ограничения неактивны. Зная это, можно было бы пренебречь ограничениями g1 и g3 и решить эту задачу как задачу с ограничениями в виде равенств, учитывая только ограничение g2(х) = b2. Из этого следует, что в точке минимума x при наличии ограничений справедливо соотношение \Lambda f(x) = \lambda \Lambda g_2(x), поскольку направление \Lambda f(x) перпендикулярно линии постоянного уровня и границе области ограничений в данной точке. (Сравните с уравнением (2.3).)


Рис. 12.1.

Возможно, что наличие ограничений будет приводить к появлению локального минимума. Это может произойти даже в том случае, когда функция имеет только одну точку минимума при отсутствии ограничений. Такая ситуация иллюстрируется рис. 12.2


Рис. 12.2.

Функция имеет только одну точку минимума при отсутствии ограничений. Однако для задачи с ограничениями обе точки A и B являются локальными минимумами, поскольку ни в одной из допустимых точек в ближайших окрестностях A или B функция не принимает меньших значений.

Некоторые из рассмотренных трудностей устраняются, если ограничиться случаем, когда область ограничений выпукла, а минимизируемая (максимизируемая) функция выпукла (вогнута).

Определим эти термины. Область является выпуклой, если отрезок прямой, соединяющей любые две точки области, принадлежит этой области. Следовательно, если x1 и x2 находятся в этой области, то любая точка вида \theta x_2 + (1-\theta)x_1, где 0 < \Theta < 1, находится в этой же области. На рис. 12.3,а изображена выпуклая область, а на рис. 12.3,б - невыпуклая.


Рис. 12.3.

Функция f(х) является выпуклой на выпуклой области X, если для любых двух точек 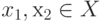x_1, х_2 \in X выполняется соотношение

f[\theta x_2 + (1-\theta)x_1] \leqslant \theta f(x_2)+(1-\theta)f(x_1) \quad \text{при} \quad 0 < \theta < 1. ( 3.1)

Для функции одной переменной это означает, что она лежит ниже хорды, соединяющей любые две точки ее графика (рис. 12.4).


Рис. 12.4.

Для вогнутой функции, определенной на выпуклом множестве, следует изменить знак неравенства, в результате чего получим соотношение

f[\theta x_2 + (1-\theta)x_1] \geqslant \theta f(x_2)+(1-\theta)f(x_1). ( 3.2)

Такая функция лежит выше хорды, соединяющей любые две точки ее графика.

Если в соотношениях (3.1) и (3.2) неравенства заменить на строгие неравенства, то функция f(х) будет строго выпуклой или строго вогнутой.

Есть еще два важных свойства выпуклых (вогнутых) функций, которые можно вывести из соотношений (3.1) и (3.2). Если функция f(х) выпукла на выпуклой области X и 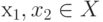х_1, x_2 \in X то

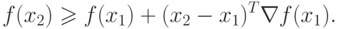f(x_2) \geqslant f(x_1) + (x_2 - x_1)^T \nabla f(x_1). ( 3.3)

Для вогнутых функций знак неравенства меняется на противоположный, что устанавливается следующим образом. Поскольку f(х) выпукла, то для 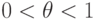0 < \theta < 1 справедливо соотношение

f[\theta x_2 + (1-\theta)x_1] \leqslant \thetaf(x_2) + (1-\theta)f(x_1)
следовательно,
f[x_1 + \theta(x_2 - x_1)] - f(x_1) \leqslant \theta [f(x_2) - f(x_1)]
и
f(x_2) \geqslant f(x_1) + \frac{f[x_1 + \theta(x_2 - x_1)]- f(x_1)}{\theta}.

Но по теореме о среднем

f[x_1 + \theta(x_2 - x_1)] = f(x_1) + \theta(x_2 - x_1)^T \nabla f[x_1 + \lambda \theta (x_2 - x_1)],
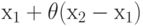где 0 < \lambda < 1, т. е. производная вычисляется в некоторой точке, лежащей между точками x1 и х_1 + \theta (х_2 - х_1).

Следовательно,

f(x_2) \geqslant f(x_1) + (x_2 - x_1)^T \nabla f[x_1 \theta \lambda (x_2 - x_1)]
и при \theta > 0 получаем соотношение (3.3).

Из соотношения (3.3) следует, что выпуклые функции одной переменной (двух переменных) лежат выше любой касательной (плоскости) к данной функции (см. рис. 12.4).

Функция выпукла, если гессиан

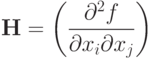
\mathbf{H} = \left( \frac{\partial^2 f}{\partial x_i \partial x_j} \right)
положительно определен. По теореме Тейлора можно записать
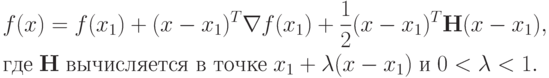
\begin{aligned} & f(x)=f(x_1)+(x-x_1)^T \nabla f(x_1) + \frac12 (x-x_1)^T \mathbf{H}(x-x_1) , \\ & \text{где} \; \mathbf{H} \; \text{вычисляется в точке} \; x_1 + \lambda(x-x_1) \; \text{и} \; 0 < \lambda < 1. \end{aligned}

Таким образом, достаточно показать, что положительно определенная квадратичная функция 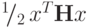^1 \! /_2 \, x^T \mathbf{H} x является выпуклой. Это сделать несложно.

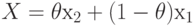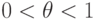Пусть x1 и x2 - произвольные значения x и пусть X = \theta х_2 + (1 - \theta)х_1, где 0 < \theta < 1.

Тогда

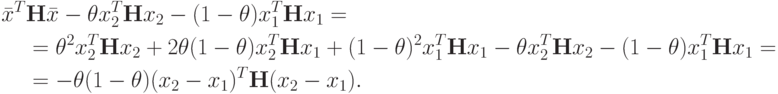
\begin{aligned} \bar{x}^T & \mathbf{H}\bar{x} - \theta x_2^T \mathbf{H} x_2 - (1-\theta) x_1^T \mathbf{H} x_1 = \\ & = \theta^2 x_2^T \mathbf{H} x_2 + 2\theta (1-\theta) x_2^T \mathbf{H} x_1 + (1 - \theta)^2 x_1^T \mathbf{H} x_1 - \theta x_2^T \mathbf{H} x_2 - (1 - \theta) x_1^T \mathbf{H} x_1 = \\ & = - \theta (1- \theta)(x_2 - x_1)^T \mathbf{H} (x_2 - x_1). \end{aligned}

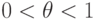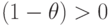Так как 0 < \theta < 1, то (1 - \theta) > 0, и если матрица Н положительно определена, то -\theta (1 - \theta) < 0. Следовательно,

[\theta x_2 + (1-\theta)x_1]^T \mathbf{H} [\theta x_2 + (1-\theta)x_1] \leqslant \theta x_2^T \mathbf{H} x_2 + (1-\theta)x_1^T \mathbf{H} x_1 . ( 3.4)

Для выпуклых функций одной переменной это означает, что вторая производная неотрицательна, поэтому первая производная является возрастающей функцией, которая может быть равна нулю только в одной точке. Следовательно, такая функция может иметь только одну точку минимума.

Дальше >>
< Лекция 11 || Лекция 12: 1234 || Лекция 13 >

Вопросы и ответы

вопросов: 0