Лекция 5: Двойственность в линейном программировании. Нахождение допустимых базисных решений. Двойственная задача линейного программирования, ее структура и свойства. Общий случай двойственности.
1. Нахождение допустимых базисных решений
Определение начального допустимого базисного решения (ДБР) в общем случае представляет значительные трудности. Поэтому для поиска ДБР разработаны специальные методы.
Метод
искусственных переменных. Пусть ограничения задачи ЛП
имеют вид  .
.
Если все  , то свободные
векторы, образующие единичную подматрицу, составляют базис, а
соответствующие им переменные - начальное базисное решение.
, то свободные
векторы, образующие единичную подматрицу, составляют базис, а
соответствующие им переменные - начальное базисное решение.
В общем случае, когда некоторые ограничения имеют знак  , например
, например
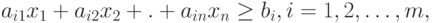
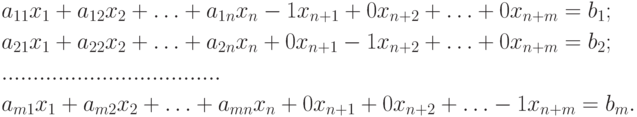 |
( 1.1) |
Свободные переменные {xn+1,.,xn+m}
в этом случае уже невозможно использовать в качестве начального базиса,
так как xn+1<0,.,xn+m<0.
Поэтому в уравнения (1.1) дополнительно вводят искусственные переменные xn+m+1,.,xn+m+k. Эти переменные не
имеют ничего общего с реальной задачей, и потому их надо вывести из
базиса как можно быстрее. Для этого перед началом итераций искусственным
переменным в целевой функции приписывают для задач максимизации очень
большие по модулю отрицательные коэффициенты (-М),
где 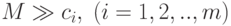 .
.
В случае решения задач минимизации искусственные переменные вводят в целевую функцию с большими положительными коэффициентами (+М).
Знаки искусственных переменных xn+m+1,.,xn+m+k должны совпадать со знаками соответствующих свободных членов. Искусственные переменные образуют начальное базисное решение. Применив симплекс-метод, необходимо вывести из базиса все искусственные переменные. Если удается доказать (или показать), что искусственные переменные полностью вывести из базиса невозможно, то это означает, что задача не имеет решения, то есть ее ограничения противоречивы.
Если на текущей итерации из базиса выводится искусственная переменная, то в следующей симплекс-таблице соответствующий ей столбец можно удалить, в дальнейших итерациях он не будет брать участия.
