Примеры моделей, получаемых из фундаментальных законов природы
По сравнению с п.1 из "Математическое моделирование. Математическая модель в задачах оптимизации. Элементарные математические модели" более подробно и для более сложных объектов рассмотрим модели, следующие из законов Архимеда, Ньютона, Кулона и других хорошо известных законов. Обсудим некоторые свойства рассматриваемых объектов.
Примеры моделей, получаемых из фундаментальных законов природы
1. Траектория всплытия подводной лодки.
Пусть подводная лодка, находящаяся в момент времени t = 0
на глубине Н от поверхности моря и движущаяся с
постоянной горизонтальной скоростью v
(рис. 2.1), получает приказ подняться
на поверхность. Если промежуток времени, за который цистерны подлодки
освобождаются от воды и заполняются воздухом, с тем чтобы ее средняя
плотность 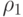 стала меньше плотности воды
стала меньше плотности воды 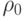 , невелик, то можно считать, что в момент t=0 на подлодку начинает действовать выталкивающая
сила, большая, чем вес лодки. По закону Архимеда выталкивающая сила
равна
, невелик, то можно считать, что в момент t=0 на подлодку начинает действовать выталкивающая
сила, большая, чем вес лодки. По закону Архимеда выталкивающая сила
равна 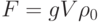 , где g -ускорение
свободного падения, V - объем подлодки. Суммарная сила,
действующая на подлодку в вертикальном направлении, - разность
между F и весом тела
, где g -ускорение
свободного падения, V - объем подлодки. Суммарная сила,
действующая на подлодку в вертикальном направлении, - разность
между F и весом тела 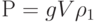 ,
а сообщаемое ею ускорение по второму закону Ньютона равно
,
а сообщаемое ею ускорение по второму закону Ньютона равно
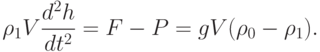
Координата I, характеризующая горизонтальное положение подлодки, изменяется по закону движения тела с постоянной скоростью:

Решая эти уравнения, находим, что
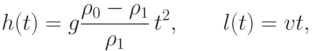 |
( 1) |
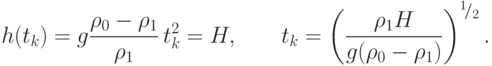
При этом в горизонтальном направлении подлодка пройдет расстояние

Исключая из (1) время, найдем траекторию движения подлодки в координатах (I, h),

Итак, непосредственное применение закона Архимеда, определяющего величину выталкивающей силы, и закона Ньютона, связывающего силу, действующую на тело, и его ускорение, позволило легко найти траекторию подлодки.
Очевидно, что параболической траекторией обладает любое движущееся в плоскости тело, имеющее по одному из направлений постоянную скорость и на которое в другом направлении действует постоянная сила (уравнения (1) фактически дают параметрическую запись параболы). К таким движениям относятся, например, полет камня, брошенного с высоты Н с горизонтальной скоростью v или полет электрона в электрическом поле плоского конденсатора. Однако в последнем случае получить траекторию тела непосредственно из фундаментальных законов нельзя, требуется применить более детальную процедуру. Рассмотрим этот вопрос подробнее.

