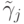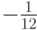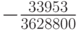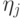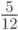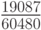НОУ ИНТУИТ | Введение в вычислительную математику. Лекция 9: Численные методы решения задачи Коши для систем обыкновенных дифференциальных уравнений

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Московский физико-технический институт

Опубликован: 25.10.2007 | Доступ: свободный | Студентов: 3916 / 1197 | Оценка: 4.50 / 4.33 | Длительность: 24:00:00

ISBN: 978-5-9556-0065-9

Темы: Алгоритмы и дискретные структуры, Математика

Специальности: Программист, Математик

|

Вам нравится? Нравится 54 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

8.3. Методы Адамса

Для решения ОДУ или систем ОДУ существуют одностадийные методы Адамса (линейные многошаговые методы), суть которых заключается в следующем.

Пусть известно приближенное решение в некоторых узлах расчетной сетки: t_n, t_{n - 1}, ..., t_{n - m}. В окрестности этих узлов заменим f(t, x(t)) интерполяционным полиномом, записанным в форме Ньютона ([8.1], [8.2], а также "Интерполяция функций" ):

f(t) = f(t_n) + f(t_n, t_{n - 1}) (t - t_n) + 
+ f(t_n, t_{n - 1}, t_{n - 2}) (t - t_n) (t - t_{n - 1}) + 
+ f(t_n, t_{n - 1}, t_{n - 2}, t_{n - 3}) (t - t_n) (t - t_{n - 1}) (t - t_{n - 2}) + ...

Для того чтобы вычислить решение в точке n + 1, запишем его в интегральном виде

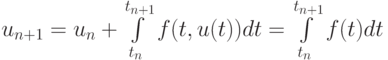
$u_{n + 1} = u_n + \int\limits_{t_n}^{t_{n + 1}}{f(t, u(t)) dt} = \int\limits_{t_n}^{t_{n + 1}}{f(t) dt}$

и подставим в него интерполяционный полином с переменным шагом

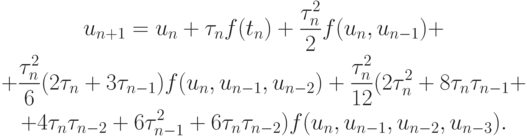
$\begin{gather*} u_{n + 1} = u_n + {\tau}_n f(t_n) + \frac{{{\tau}_n^2 }}{2} f(u_n, u_{n - 1}) + \\ + \frac{{{\tau}_n^2 }}{6} (2{\tau}_n + 3{\tau}_{n - 1}) f(u_n, u_{n - 1}, u_{n - 2}) + \frac{{{\tau}_n^2 }}{{12}} (2{\tau}_n^2 + 8{\tau}_n {\tau}_{n - 1} + \\ + 4{\tau}_n {\tau}_{n - 2} + 6{\tau}_{n - 1}^2 + 6{\tau}_n {\tau}_{n - 2})f(u_n, u_{n - 1}, u_{n - 2}, u_{n - 3}). \end{gather*}$

Здесь $\tau _{n} = t_{n + 1} - t_{n}, f(u_{n}, u_{n - 1}), f(u_{n}, u_{n - 1}, u_{n - 2})$ и т.д. - разделенные разности.

Эта формула четвертого порядка точности. Если опустить последнее слагаемое, то получим формулу третьего порядка, если опустить еще и предпоследнее, то — второго, и т.д. Если же положить $\tau _{n} = const,$ то формула значительно упростится:

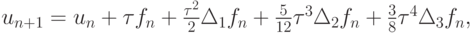
$u_{n + 1} = u_n + {\tau}f_n + \frac{{{\tau}^2 }}{2} \Delta_1 f_n + \frac{5}{{12}} {\tau}^3 \Delta_2 f_n + \frac{3}{8} {\tau}^4 \Delta_3 f_n,$

где $\Delta _{k}f_{n}$ — k - я конечная разность.

Для того чтобы начать вычисления по данному варианту метода Адамса, необходимо знать решение в четырех точках. Это можно сделать, например, с помощью методов Рунге - Кутты. Кроме того, коэффициент при погрешности, например, для метода четвертого порядка точности Рунге - Кутты существенно меньше соответствующего коэффициента для метода Адамса.

Первые четыре метода Адамса, от первого до четвертого порядка точности с постоянным шагом интегрирования, представляются в виде

$\left. \begin{array}{l} u_{n + 1} = u_n + {\tau}f_n, \\ u_{n + 1} = u_n + {\tau}\left({\frac{3}{2} f_n - \frac{1}{2} f_{n - 1}}\right), \\ u_{n + 1} = u_n + {\tau}\left({\frac{23}{12}f_n - \frac{16}{12} f_{n - 1} + \frac{5}{12} f_{n - 2}}\right) \\ u_{n + 1} = u_n + {\tau}\left({\frac{55}{24} f_n - \frac{59}{24} f_{n - 1} + \frac{37}{24} f_{n - 2} - \frac{9}{24} f_{n - 3}}\right). \end{array} \right.$

( 8.7)

В общем виде методы Адамcа могут быть записаны следующим образом:

$u_{n + 1} = u_n + {\tau}\sum\limits_{j = 0}^{k - 1}{\eta_j \Delta^{j} f_j}.$

Значительно большее значение в вычислительной практике имеют неявные методы Адамса, которые можно записать как

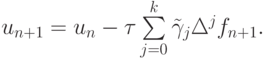
$u_{n + 1} = u_n - {\tau}\sum\limits_{j = 0}^{k}{\tilde {\gamma}_j {\Delta}^{j} f_{n + 1}}.$

Первые четыре неявных метода имеют вид

$\left. \begin{array}{l} k = 0: u_{n + 1} = u_n + {\tau}f_{n + 1}, \\ k = 1: u_{n + 1} = u_n + {\tau}\left({\frac{1}{2} f_{n + 1} + \frac{1}{2} f_n}\right), \\ k = 2: u_{n + 1} = u_n + {\tau}\left({\frac{5}{{12}}f_{n + 1} + \frac{8}{{12}} f_n - \frac{1}{{12}} f_{n - 1}}\right), \\ k = 3: u_{n + 1} = u_n + {\tau}\left({\frac{9}{{24}} f_{n + 1} + \frac{{19}}{{24}} f_n - \frac{5}{{24}} f_{n - 1} + \frac{1}{{24}} f_{n - 2}}\right). \end{array} \right.$

Первая и вторая формулы — неявный метод Эйлера и неявный метод трапеций соответственно. Порядок аппроксимации приведенных методов — с первого по четвертый соответственно.

Таблица 8.18.
j	0	1	2	3	4	5	6	7	8
$\tilde {\gamma}_j$	1	$- \frac{1}{2}$	$- \frac{1}{12}$	$- \frac{1}{24}$	$- \frac{19}{720}$	$- \frac{3}{160}$	$- \frac{863}{60 480}$	$- \frac{275}{24 192}$	$- \frac{33 953}{3 628 800}$

Таблица 8.19.
j	0	1	2	3	4	5	6	7	8
$\eta _{j}$	1	$\frac{1}{2}$	$\frac{5}{12}$	$\frac{3}{8}$	$\frac{251}{720}$	$\frac{95}{288}$	$\frac{19 087}{60 480}$	$\frac{5 257}{17 280}$	$\frac{1 070 017}{3 628 800}$

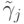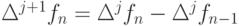Для k = 8 коэффициент $\tilde {\gamma}_j$ можно представить в виде таблицы (табл. 8.19) и ввести следующие обозначения: $\Delta ^{j + 1}f_{n} = \Delta ^{j}f_{n} - \Delta ^{j}f_{n - 1}$ — "разности назад", $\eta ^{j}$ — коэффициенты, которые можно представить в виде таблицы (для k = 8 табл. 8.2). Для k = 1 получается уже знакомый явный метод Эйлера.

Дальше >>

Авторизоваться

Введение в вычислительную математику

Численные методы решения задачи Коши для систем обыкновенных дифференциальных уравнений

8.3. Методы Адамса

Вопросы и ответы