НОУ ИНТУИТ | Введение в вычислительную математику. Лекция 9: Численные методы решения задачи Коши для систем обыкновенных дифференциальных уравнений

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Московский физико-технический институт

Опубликован: 25.10.2007 | Доступ: свободный | Студентов: 3914 / 1195 | Оценка: 4.50 / 4.33 | Длительность: 24:00:00

ISBN: 978-5-9556-0065-9

Темы: Алгоритмы и дискретные структуры, Математика

Специальности: Программист, Математик

|

Вам нравится? Нравится 54 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

8.5. Устойчивость методов Рунге - Кутты

Для исследования устойчивости методов Рунге - Кутты для численного решения задачи

$\frac{d{u}}{dt} = f(t, u), \quad u(0) = u_0$

представим ее дискретный аналог в виде

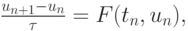$\frac{u_{n + 1} - u_n}{{\tau}} = F(t_n, u_n),$

( 8.8)

здесь F(t, x) — функция приращения метода Рунге - Кутты, которая, конечно, связана с функцией правой части системы ОДУ.

Теорема 2 ( Устойчивость методов Рунге - Кутты [8.3], [8.9]). Пусть f(t, x) Липшиц - непрерывна по второму аргументу, т.е.

$\|f(t, x) - f(t, y)\| \le C\|x - y\|,$

причем это условие выполняется для каждого t, $C \ne C({\tau})$ и $C{\tau}\ll 1.$

Тогда разностное уравнение (8.8) устойчиво и имеет место оценка

$\|u_n - v_n\| \le e^{C_2t}\|u_0 - v_0\| + \frac{2\varepsilon e^{C_2t}}{C_2}.$

( 8.9)

Здесь u_n, v_n - решения близких систем разностных уравнений:

$\begin{gather*} \frac{u_{n + 1} - u_n}{{\tau}} = F(t_n, u_n) + \varepsilon_n^1, u_0 = u^0, \\ \frac{{v_{n + 1} - v_n}}{{\tau}} = {F}(t_n, v_n) + \varepsilon_n^2, v_0 = v^0 \end{gather*}$

и $\varepsilon$ — максимальная погрешность при вычислении правой части системы, т.е. для всех n (включая нуль)

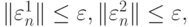
$\|\varepsilon^1_n\| \le \varepsilon, \|\varepsilon^2_n\| \le \varepsilon,$

а постоянная C₂ незначительно отличается от C.

Сформулируем вначале следующую лемму.

Лемма 1. Пусть C — постоянная Липшица для функции правых частей системы (8.1), тогда функция приращения F(t, u) для метода (8.8) удовлетворяет следующему неравенству:

$\|F(t, u_n) - F(t, v_n)\| \le C_2\|u_n - v_n\|,$

где

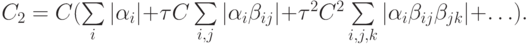
$C_2 = C(\sum\limits_i|\alpha_i| + {\tau}C\sum\limits_{i, j}|\alpha_i\beta_{ij}| + {\tau}^2C^2\sum\limits_{i, j, k}|\alpha_i\beta_{ij}\beta_{jk}| + \ldots).$

Суммирование в правой части последнего равенства ведется по каждому индексу от 1 до r > — числа стадий метода. Число сумм в скобках, конечно, тоже равно r >. Отметим также, что если в таблице Бутчера все коэффициенты неотрицательны (такой метод Рунге - Кутты, по аналогии с методом численного интегрирования, назовем правильным), то из условий порядка ( аппроксимации ) будет следовать, что в скобках стоят первые r > членов разложения $e^{C\tau }$ в ряд Тейлора. Отсюда необходимое требование (в формулировке теоремы) к малости $C\tau.$ В случае наличия отрицательных коэффициентов в таблице Бутчера константа Липшица C₂ увеличится незначительно — число стадий метода конечно и невелико (в настоящее время известны методы максимум с 17 стадиями, [8.6]).

Доказательство данной леммы довольно простое, но громоздкое. Читатель может проделать это самостоятельно.

Доказательство теоремы.

Рассмотрим эти близкие уравнения. Вычитая из первого уравнения второе, получим

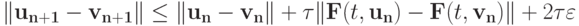${\|\mathbf{u_{n + 1}} - \mathbf{v_{n + 1}}\| \le\|\mathbf{u_n} - \mathbf{v_n}\| + {\tau}\|\mathbf{F}(t, \mathbf{u_n}) - \mathbf{F}(t, \mathbf{v_n})\| + 2{\tau}\varepsilon}$

( 8.10)

или, учитывая условие Липшица,

$\|\mathbf{u_{n + 1}} - \mathbf{v_{n + 1}}\| \le (1 + C_2{\tau})\|\mathbf{u_n} - \mathbf{v_n}\| + 2{\tau}\varepsilon.$

Здесь константа C₂ — постоянная Липшица функции приращения метода Рунге - Кутты, выражение для нее приведено выше в формулировке леммы 8.1.

Далее, применяя последовательно это неравенство, получим оценки:

$\begin{gather*} \|\mathbf{u_1} - \mathbf{v_1}\| \le (1 + C_2{\tau})\|\mathbf{u_0} - \mathbf{v_0}\| + 2{\tau}\varepsilon, \\ \|\mathbf{u_2} - \mathbf{v_2}\| \le (1 + C_2{\tau})\|\mathbf{u_1} - \mathbf{v_1}\| + 2{\tau}\varepsilon \le {(1 + C_2{\tau})}^2\|\mathbf{u_0} - \mathbf{v_0}\| + 2{\tau}\varepsilon[1 + (1 + C_2{\tau})], \\ \|\mathbf{u_3} - \mathbf{v_3}\| \le (1 + C_2{\tau})\|\mathbf{u_2} - \mathbf{v_2}\| + 2{\tau}\varepsilon \le \\ \le {(1 + C_2{\tau})}^3\|\mathbf{u_0} - \mathbf{v_0}\| + 2{\tau}\varepsilon[1 + (1 + C_2{\tau}) + {(1 + C_2{\tau})}^2], \\ \|\mathbf{u_n} - \mathbf{v_n}\| \le {(1 + C_2{\tau})}^{n}\|\mathbf{u_0} - \mathbf{v_0}\| + 2{\tau}\varepsilon[1 + (1 + C_2{\tau}) + \ldots + {(1 + C_2{\tau})}^{n - 1}], \end{gather*}$

откуда, после суммирования прогрессии, имеем

$\begin{gather*} \|\mathbf{u_n} - \mathbf{v_n}\| \le {(1 + C_2{\tau})}^{n}\|\mathbf{u_0} - \mathbf{v_0}\| + 2{\tau}\varepsilon\frac{{(1 + C_2{\tau})}^{n} - 1}{(1 + C_2{\tau}) - 1} \le \\ \le {(1 + C_2{\tau})}^{n}[\|\mathbf{u_0} - \mathbf{v_0}\| + \frac{2\varepsilon}{C_2}]. \end{gather*}$

Далее полагаем $(1 + C_{2}\tau )^{n} = (1 + C_{2}\tau )^{t/\tau } \approx$ $e^{C_2t}$ при $C_2 {\tau}\ll 1.$

После подстановки экспоненты в последнюю оценку получим неравенство (8.9).

Заметим, что экспоненциальный множитель в неравенстве (8.9) при больших t велик, а оценка, в наиболее общем случае, в предположении Липшиц - непрерывности функции $\mathbf{F}(\mathbf{u}),$ неулучшаема. Однако в некоторых важных частных случаях эту оценку можно улучшить, рассматривая более тонкие свойства рассматриваемой функции. Докажем следующее утверждение [8.9], рассматривая задачу Коши для системы ОДУ.

Утверждение. Пусть матрица

$A(u) = \frac{1}{2} (f_u (u ) + f_u^*(u))$

строго отрицательна, т.е.

$(A(u)\xi, \xi) \le - a(\xi, \xi)$

для любых $\xi , u$ и a > 0 (траектория, в окрестности которой выполняется это условие, называется устойчивой ).

Тогда при интегрировании правильным методом Рунге - Кутты k - го порядка аппроксимации погрешность приближенного решения есть $O(\tau ^{k})$ при любом t > 0 при выполнении условий $a{\tau}\ll 1.$

Утверждение будет доказано, если в оценке устойчивости метода не будет содержаться множитель e^Ct.

Дальше >>

Авторизоваться

Введение в вычислительную математику

Численные методы решения задачи Коши для систем обыкновенных дифференциальных уравнений

8.5. Устойчивость методов Рунге - Кутты

Вопросы и ответы