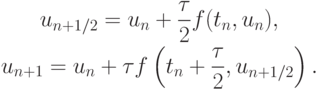НОУ ИНТУИТ | Введение в вычислительную математику. Лекция 9: Численные методы решения задачи Коши для систем обыкновенных дифференциальных уравнений

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Московский физико-технический институт

Опубликован: 25.10.2007 | Доступ: свободный | Студентов: 3974 / 1245 | Оценка: 4.50 / 4.33 | Длительность: 24:00:00

ISBN: 978-5-9556-0065-9

Темы: Алгоритмы и дискретные структуры, Математика

Специальности: Программист, Математик

|

Вам нравится? Нравится 54 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Таким образом, можно написать приближенное равенство:

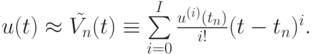
$u(t) \approx \tilde {V_n} (t) \equiv \sum\limits_{i = 0}^{I} {\frac{u^{(i)} (t_n)}{i!} (t - t_n)^{i}. }$

Полагая

$u_{n + 1} = \tilde {V_n} (t_{n + 1}),$

получаем приближенное значение u(t) в точке t = t_{n +
1}. При I = 1 и $t_{n + 1} - t_{n} = \tau = const$ получаем метод Эйлера:

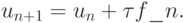
$u_{n + 1} = u_{n} + \tau f\_ n.$

Этот способ не получил распространения в практике решения дифференциальных уравнений из - за необходимости вычисления производных u⁽ⁱ⁾, где $i = 1 \div I.$ По затратам машинного времени он заметно уступает другим методам, о которых будет идти речь далее.

В настоящее время в практике решения жестких систем ОДУ применяют так называемые многозначные методы, основанные на разложении в ряд Тейлора и вычислении производных. О жестких системах ОДУ будет рассказано ниже.

Рассмотрим еще один способ получения простейших одношаговых расчетных схем для численного решения уравнения (8.1), для чего напишем равенство

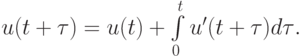
$u(t + {\tau}) = u(t) + \int\limits_0^{t}{u^{\prime}(t + {\tau}) d{\tau}}.$

После аппроксимации интеграла в правой части по формуле прямоугольников и замене его на величину 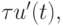$\tau u'(t),$ получим

$u(t + \tau ) = u(t) + \tau u'(t) + O(\tau ^{2}),$

или

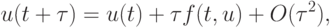
$u(t + \tau ) = u(t) + \tau f(t, u) + O(\tau ^{2}),$

поскольку u'(t) = f(t, u).

Опуская член 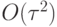$O(\tau ^{2})$ и обозначая 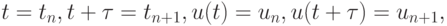$t = t_{n}, t + \tau = t_{n + 1}, u(t) = u_{n}, u(t + \tau ) = u_{n + 1},$ получим метод Эйлера.

Если рассматриваемый интеграл заменить формулой трапеций, получим

$u(t + {\tau}) = u(t) + \frac{{\tau}}{2} [u^{\prime}(t) + u^{\prime}(t + {\tau})] + O({\tau}^3 ),$

откуда имеем

$u_{n + 1} = u_n + \frac{{\tau}}{2} [f(t_n, u_n) + f(t_{n + 1}, u_{n + 1})].$

Этот метод называется неявным методом трапеций. Для того чтобы метод был явным, его делают двухэтапным:

$\begin{gather*} \tilde u_{n + 1} = u_n + {\tau}f(f_n, u_n), \\ u_{n + 1} = u_n + \frac{{\tau}}{2}[f(t_n, u_n) + f(t_{n + 1}, \tilde u_{n + 1})], \end{gather*}$

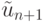где $\tilde u_{n + 1}$ — вспомогательная величина, вычисляемая на промежуточном этапе. Если этот же интеграл приблизить формулой прямоугольников со средней точкой, то получим

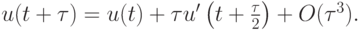
$u(t + {\tau}) = u(t) + {\tau}u^{\prime}\left({t + \frac{{\tau}}{2}}\right) + O({\tau}^3 ).$

Снова воспользовавшись дифференциальным уравнением (8.1), преобразуем последнее выражение к виду

$u(t + {\tau}) = u(t) + {\tau}f\left[{t + \frac{{\tau}}{2}, u\left({t + \frac{{\tau}}{2}}\right)}\right] + O({\tau}^3 ).$

Соответствующий неявный метод имеет вид

$u_{n + 1} = u_n + {\tau}f\left[{t_n + \frac{{\tau}}{2}, u\left({t_n + \frac{{\tau}}{2}}\right)}\right] ;$

для его явной реализации можно воспользоваться следующей двухэтапной формулой:

$\begin{gather*} u_{n + 1/2} = u_n + \frac{{\tau}}{2} f(t_n, u_n), \\ u_{n + 1} = u_n + {\tau}f\left({t_n + \frac{{\tau}}{2}, u_{n + 1/2}}\right). \end{gather*}$

Дальше >>

Авторизоваться

Введение в вычислительную математику

Численные методы решения задачи Коши для систем обыкновенных дифференциальных уравнений

Вопросы и ответы