Численные методы решения экстремальных задач
4.3. Задачи математического программирования
Под линейным программированием понимают часть экстремальных задач, рассматривающую минимизацию линейных функций и переменных при наличии дополнительных линейных условий трех типов:
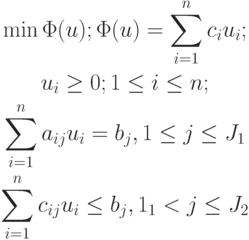 |
( 4.3) |
Каждое из этих условий определяет полупространство, ограниченное гиперплоскостью; вместе эти условия определяют выпуклый n -мерный
многогранник J', являющейся пересечением полупространств. Условия типа равенств выделяют из n - мерного пространства (n - m) -мерную плоскость. Ее пересечение с M дает выпуклый (n - m) -мерный многогранник G. Таким образом, задача состоит в том, чтобы найти минимум линейной функции 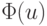 в многограннике G.
в многограннике G.
G — выпуклый многогранник (возможно и неограниченный),
поэтому внутри него линейная функция 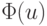 не может достигать минимума. Показывается, что ее минимум, если он существует, достигается в какой-то
из его вершин. Теоретически задача линейного программирования достаточно проста: необходимо вычислить значение функций в конечном числе точек — вершинах
многогранника, сравнить их между собой и найти среди них наименьшее. Однако трудность заключается в том, что в экономических задачах количество переменных порядка
не может достигать минимума. Показывается, что ее минимум, если он существует, достигается в какой-то
из его вершин. Теоретически задача линейного программирования достаточно проста: необходимо вычислить значение функций в конечном числе точек — вершинах
многогранника, сравнить их между собой и найти среди них наименьшее. Однако трудность заключается в том, что в экономических задачах количество переменных порядка 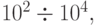 поэтому решение оказывается достаточно
сложным.
поэтому решение оказывается достаточно
сложным.
Пример. Рассмотрим следующую простую задачу линейной оптимизации на плоскости: найти 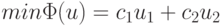 при ограничениях
при ограничениях
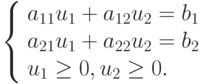
Неравенства 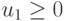 и
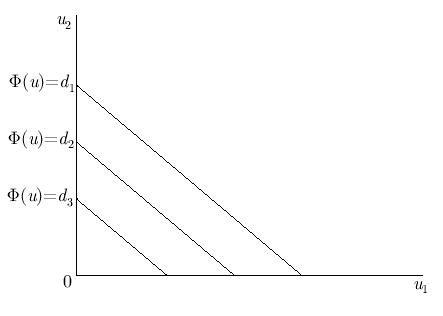
и 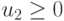 выделяют I квадрант плоскости (u1, u2), а линейная функция
выделяют I квадрант плоскости (u1, u2), а линейная функция  при определенных c1, c2 задает в этом квадранте семейство прямых уравнением c1u1 + c2u2 = d ( d неизвестно) (рис. 4.10).
при определенных c1, c2 задает в этом квадранте семейство прямых уравнением c1u1 + c2u2 = d ( d неизвестно) (рис. 4.10).
Вообще говоря, ограничения в форме равенств могут быть следующего типа: отсутствует, одно ограничение, два ограничения (последний случай соответствуют
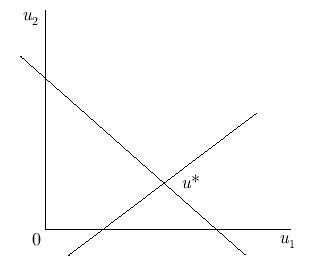
рассматриваемому). Пусть СЛАУ в данном примере имеет единственное решение 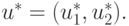
Если выполнены неравенства 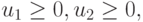 то u* и есть решение задачи линейной оптимизации, а
то u* и есть решение задачи линейной оптимизации, а 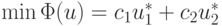 (рис. 4.11).
(рис. 4.11).
Если же, например, 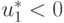 и
и 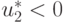 то задача линейного программирования неразрешима, так как по условию решения находится внутри первого квадранта. В данном случае ограничения определяют единственное решение рассматриваемой задачи, а целевая функция принимает "навязанное" значение
то задача линейного программирования неразрешима, так как по условию решения находится внутри первого квадранта. В данном случае ограничения определяют единственное решение рассматриваемой задачи, а целевая функция принимает "навязанное" значение 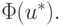 Процесс решения оказался весьма простым. Если бы имелось больше условий типа неравенств и меньше равенств, рассмотрение оказалось бы более сложным.
Процесс решения оказался весьма простым. Если бы имелось больше условий типа неравенств и меньше равенств, рассмотрение оказалось бы более сложным.
Пример. Графическое решение задачи
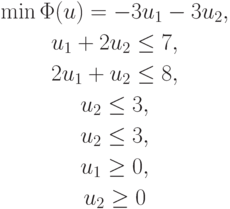
приводит к решению u* = (3, 2) и  Для решения задачи рассматриваются линии уровня функции
Для решения задачи рассматриваются линии уровня функции 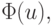 т.е. семейство параллельных прямых - 3u1 - 3u2 = d = const.
т.е. семейство параллельных прямых - 3u1 - 3u2 = d = const.
Нормальный к этим прямым вектор 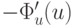 указывает направление убывания целевой функции. Решением задачи u* является одна из вершин многогранника, образованного прямыми системы неравенств.
указывает направление убывания целевой функции. Решением задачи u* является одна из вершин многогранника, образованного прямыми системы неравенств.
4.4. Задачи
- Свести задачу о нахождении решения системы нелинейных уравнений
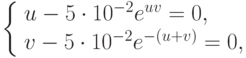
к вариационной задаче в области
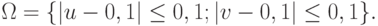
Решение. Решение системы сводится к нахождению условий минимума функционала
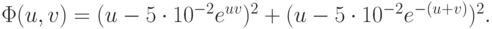
- Свести задачу о нахождении минимума функции
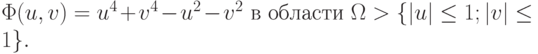
к решению системы алгебраических уравнений.
Решение. Задача о нахождении минимума функции
 сводится к решению системы уравнений
сводится к решению системы уравнений 
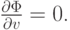
- Найти значения {x, y}, при которых достигается минимум функции f(x,y) = x3 + y3 - 3xy.
Решение. Вычислим частные производные
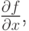 и приравняем их к нулю. Получим систему двух нелинейных уравнений 3x2 - 3y = 0, - 3x + 3y2 = 0. Решениями этой системы являются пары {0, 0}, {1, 1}. Подстановкой убеждаемся, что вторая точка является точкой глобального минимума.
и приравняем их к нулю. Получим систему двух нелинейных уравнений 3x2 - 3y = 0, - 3x + 3y2 = 0. Решениями этой системы являются пары {0, 0}, {1, 1}. Подстановкой убеждаемся, что вторая точка является точкой глобального минимума.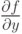
- Методом деления отрезка пополам найти точку локального минимума для функции f(x) = x3 + e - x - x на отрезке [0, 1] с точностью

Решение. Обозначим границы отрезка a0 = 0, b0 = 1 и зададим
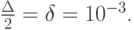
Вычислим
и Так как второе значение меньше первого, то положим {a1, b1 } = {0.4990, 1} . Продолжая далее, получим {a2, b2 } = {0,4990; 0,7505}, {a3, b3} = {0,6238; 0,7505}, {a4, b4} = {0,6861; 0,7505}, {a5, b5 } = {0,6861; 0,7191}, {a6, b6 } = {0,7016; 0,7191}, {a7, b7 } = {0,7101; 0,7198} .
Так как второе значение меньше первого, то положим {a1, b1 } = {0.4990, 1} . Продолжая далее, получим {a2, b2 } = {0,4990; 0,7505}, {a3, b3} = {0,6238; 0,7505}, {a4, b4} = {0,6861; 0,7505}, {a5, b5 } = {0,6861; 0,7191}, {a6, b6 } = {0,7016; 0,7191}, {a7, b7 } = {0,7101; 0,7198} .
- С помощью метода Ньютона найти минимум функции F(t) = sin t -
cos t, t0 = - 0,5.
Решение. Найдем точку минимума функции F(t) как корень уравнения F'(t) = 0. Для этого построим итерационный процесс Ньютона:
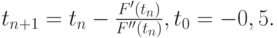
При t0 = - 0,5 имеем
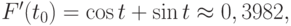
 Дальнейшие вычисления дают t2 = - 0,7854, t3 = - 0,7854.
Дальнейшие вычисления дают t2 = - 0,7854, t3 = - 0,7854.
4.5. Задачи для самостоятельного решения
- Найти точку локального минимума функций:
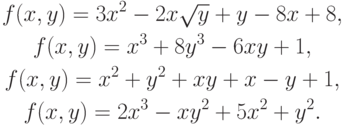
- Найти точку локального минимума функций:
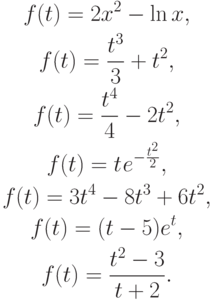
используя методы дихотомии и сведения вариационной задачи к решению алгебраического уравнения.
- Найти точки локального минимума функций
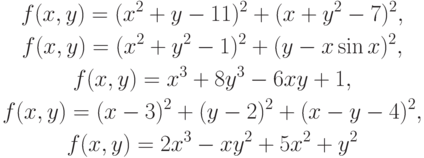
методом покоординатного спуска.