Численные методы решения экстремальных задач
Можно показать, что покоординатный спуск реализуется (сходится к точке минимума) при условии существования вторых производных 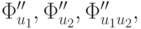 причем
причем  Изломы приводят к подъему. Этот метод сходится достаточно медленно, а при наличии так называемых "оврагов", очень медленно. Разделим "рельефы", образуемые линиями уровня — на два типа: "котловинный" и "овражный". В первом случае линии уровня похожи на эллипсы, а функция вблизи своего минимума практически не изменяется при изменении переменных. Этот случай можно назвать простым (рис. 4.4).
Изломы приводят к подъему. Этот метод сходится достаточно медленно, а при наличии так называемых "оврагов", очень медленно. Разделим "рельефы", образуемые линиями уровня — на два типа: "котловинный" и "овражный". В первом случае линии уровня похожи на эллипсы, а функция вблизи своего минимума практически не изменяется при изменении переменных. Этот случай можно назвать простым (рис. 4.4).
Рельеф овражного типа имеет либо точки излома (рис. 4.4), либо участки с большей кривизной ("разрешимый овраг"). Если линии уровня — кусочно - гладкие, то выделим на них точки излома, геометрическое место которых назовем истинным "оврагом", если угол направлен в сторону возрастания функции — и "гребнем", если в сторону убывания (рис. 4.5).\vspace{- 4mm}
Примером разрешимого оврага является функция 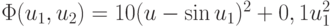 (рис. 4.6 ).
(рис. 4.6 ).
Неупорядоченный тип рельефа характеризуется наличием многих экстремумов;
примером может служить функция  (рис. 4.7).
(рис. 4.7).
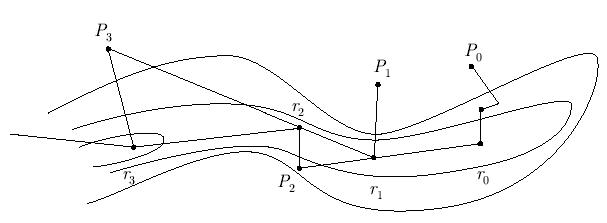
Метод оврагов используется в случае, если "дно" оврага узкое, а "склоны" крутые. В этом случае спустимся из двух точек P0 и P1, например, с помощью метода координатного или градиентного спуска на "дно" оврага (или в его окрестность) в точки с координатами r0 или r1, не требуя высокой точности сходимости. Проведем через эти две точки прямую и выберем на ней новую точку

где h = const > 0 — "овражный шаг", который выбирается для каждой функции путем расчета (рис. 4.8). Точка лежит на "склоне" оврага. Из нее спускаемся на "дно" и попадаем в некую точку r2, через точки r1 и r2 проводим прямую и находим точку P3, из которой возможно опуститься в точку r3.
Процесс продолжается до тех пор, пока значения целевой функции на "дне" оврага убывают, т.е. пока