Численные методы решения экстремальных задач
Теорема. Пусть функция 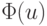 дважды непрерывно
дифференцируема. Тогда достаточным условием того, чтобы стационарная точка u* была точкой локального минимума, является положительная определенность матрицы Гессе
дважды непрерывно
дифференцируема. Тогда достаточным условием того, чтобы стационарная точка u* была точкой локального минимума, является положительная определенность матрицы Гессе
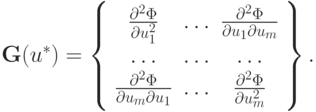
Отметим, что методы отыскания минимума 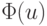 нередко оказываются более эффективными, чем методы численного решения СНАУ.
нередко оказываются более эффективными, чем методы численного решения СНАУ.
Метод перебора.
Пусть U = [a, b] , т.е. отрезок числовой оси. Разобьем его на n равных частей с узлами в точках ui = a + i(b - a)/n; i = 0, ..., n.
Вычислив значение 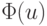 в этих точках, найдем путем сравнения точку u*, в которой
в этих точках, найдем путем сравнения точку u*, в которой

Далее полагаем: 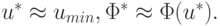 Погрешность в определении u* этого простейшего метода не превосходит числа
Погрешность в определении u* этого простейшего метода не превосходит числа
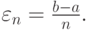
Этот метод прост, но неэкономичен, особенно когда ищется минимум функции многих переменных. Например, в гиперкубе 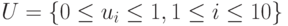 с разбиением каждого из отрезков (по каждой из координат) на 10 частей, с быстродействием
с разбиением каждого из отрезков (по каждой из координат) на 10 частей, с быстродействием  операций в секунду потребуется около 107 с (примерно 4 месяца) для нахождения
операций в секунду потребуется около 107 с (примерно 4 месяца) для нахождения 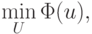 если предположить, что количество арифметических действий, необходимое для вычисления значений
если предположить, что количество арифметических действий, необходимое для вычисления значений 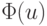 в каждой точке требует тысячи арифметических операций. Этот метод можно сделать более эффективным, если сначала определить минимум с грубым шагом, затем уже искать минимум с меньшим шагом на том из отрезков [xi, xi + 1], на котором
предполагается наличие минимума; можно и далее уточнять решение задачи таким же образом.
в каждой точке требует тысячи арифметических операций. Этот метод можно сделать более эффективным, если сначала определить минимум с грубым шагом, затем уже искать минимум с меньшим шагом на том из отрезков [xi, xi + 1], на котором
предполагается наличие минимума; можно и далее уточнять решение задачи таким же образом.
Усовершенствованием этого метода являются методы исключения отрезков,
дихотомии (деления отрезка пополам) и золотого сечения. В них отрезок [a, b] делится на 4 части выбором внутри отрезка точек u1, u2, в которых вычисляются значения целевой функции. Сравнив ее значения в этих точках, можно сократить отрезок поиска точки минимума, перейдя к отрезку [a, u2], если  или [u1, b], если
или [u1, b], если  Эту процедуру можно продолжить.
Эту процедуру можно продолжить.
В методе дихотомии точки u1, u2 выбираются близко к середине отрезка
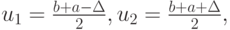
 достаточно мало. Поскольку отношение
достаточно мало. Поскольку отношение 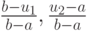
В конце вычисления в качестве приближенного значения u* берется середина последнего отрезка. В результате n итераций длина отрезка будет
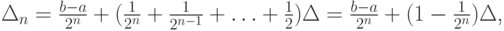

Находя n из условия  получим количество итераций, необходимое для достижения данной точности
получим количество итераций, необходимое для достижения данной точности
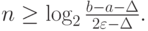
Если в предыдущем неравенстве положить  малой, то
малой, то
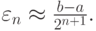
Метод золотого сечения.
Расположим точки u1, u2 на [a, b] так, чтобы одна из них стала бы также пробной, но уже на новом отрезке, после исключения части исходного отрезка. Это позволит уменьшить количество вычислений, поскольку необходимо будет вычислить значение 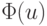 лишь в одной из пробных точек, так как во второй оно уже известно.
лишь в одной из пробных точек, так как во второй оно уже известно.
Найдем расположение таких точек, для чего рассмотрим отрезок [0, 1] и, для определенности, положим, что при его уменьшении исключается его правая часть.
