Численные методы решения экстремальных задач
4.2.2. Метод градиентного спуска
Напомним, что градиент функции

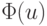 в данной точке. В точке минимума
в данной точке. В точке минимума 
Построим итерационный процесс следующим образом:
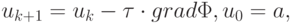
где 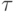 — шаг спуска (итерационный параметр). Итерации
продолжим до выполнения заданного условия окончания процесса поиска минимума, например
— шаг спуска (итерационный параметр). Итерации
продолжим до выполнения заданного условия окончания процесса поиска минимума, например

Пример. Рассмотрим функцию двух переменных

В соответствии с методом градиентного спуска получим
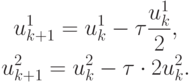
Пусть начальное приближение u0 = {1;1} ; 
Тогда u1 = {0,95; 0,80} ; u2 =
{0,9025; 0,6400} ; u3 = {0,8574; 0,5120} ; 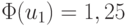 ;
; 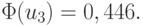
Если взять 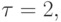 то u1 = {0; - 3} и
то u1 = {0; - 3} и 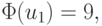 в то время как
в то время как 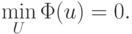 Выбор шага оказывается существенным в этом методе, поэтому чаще используются методы с переменным шагом.
Выбор шага оказывается существенным в этом методе, поэтому чаще используются методы с переменным шагом.
4.2.3. Метод наискорейшего спуска
В методе градиентного спуска выберем шаг 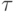 так, чтобы
функция
так, чтобы
функция 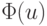 максимально уменьшала свое значение:
максимально уменьшала свое значение:

В предыдущем примере выбор шага в точке u0 сводится к задаче о поиске минимума функции
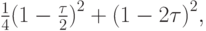
откуда 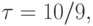 поскольку
поскольку
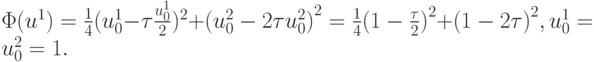
На следующих шагах 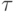 будет зависеть от
будет зависеть от 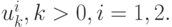
Общий случай этого метода, а также метод сопряженных градиентов рассмотрены в "Численное решение систем линейных алгебраических уравнений" .
Отметим следующее важное обстоятельство. Решение экстремальных задач в Ln зачастую сопряжено со значительными трудностями, особенно для многоэкстремальных задач. Некоторые из этих трудностей исчезают, если ограничиться рассмотрением только выпуклых функций на выпуклых множествах.
Определение. Функция 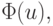 заданная на выпуклом
множестве
заданная на выпуклом
множестве 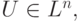 называется выпуклой, если для любых точек
называется выпуклой, если для любых точек 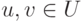 и любого
и любого ![\alpha \in \left[ {0,1}\right]](/sites/default/files/tex_cache/c4f71976a1dffa72e25b241a1eff19b8.png) выполнено:
выполнено:
![\Phi \left[{\alpha u + (1 - \alpha )v}\right] \le \alpha \Phi (u) + (1 - \alpha )\Phi (v).](/sites/default/files/tex_cache/64763b3416ed8939bab3b04e70912f3c.png)
Определение. Функция 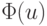 называется строго выпуклой, если для всех
называется строго выпуклой, если для всех  выполнено строгое неравенство
выполнено строгое неравенство
![\Phi \left[{\alpha u + (1 - \alpha )v}\right] <\alpha \Phi (u) + (1 - \alpha )\Phi (v).](/sites/default/files/tex_cache/9485d835c81044d9b72b864a7824758f.png)
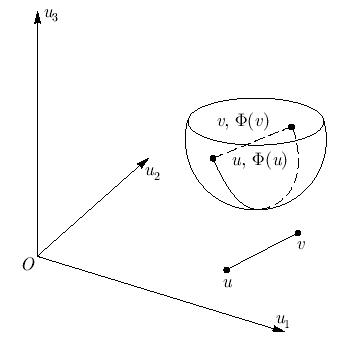
Это определение имеет наглядный геометрический смысл: график функции 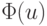 на интервале, соединяющем точки u, v лежит ниже хорды, проходящей через точки
на интервале, соединяющем точки u, v лежит ниже хорды, проходящей через точки 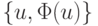 и
и  (рис. 4.11).
(рис. 4.11).
Для дважды непрерывно дифференцируемой функции 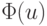 положительная определенность матрицы Гессе
положительная определенность матрицы Гессе 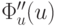 есть достаточное условие строгой выпуклости.
есть достаточное условие строгой выпуклости.
Теорема. Пусть 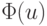 — выпуклая функция на
выпуклом множестве U,
— выпуклая функция на
выпуклом множестве U,  Тогда любой ее локальный минимум на U является одновременно и глобальным.
Тогда любой ее локальный минимум на U является одновременно и глобальным.
Глобальный минимум строго выпуклой функции 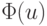 на выпуклом
множестве U достигается в единственной точке.
на выпуклом
множестве U достигается в единственной точке.
Доказательство.
Предположим противное, т.е. u0 — точка локального, а u* — глобального минимума 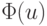 на U,
на U, 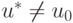 и
и 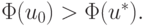 Отсюда, с учетом выпуклости
Отсюда, с учетом выпуклости 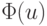 имеем
имеем
![\Phi \left[{\alpha u* + (1 - \alpha )u_0}\right] \le \alpha\Phi (u*) + (1 - \alpha )\Phi (u_0) <\Phi (u_0).](/sites/default/files/tex_cache/1989220d2f2658a1787b742560120ab5.png)
При  точка
точка 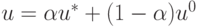 попадает в сколь угодно малую окрестность u0. Поэтому полученное неравенство
попадает в сколь угодно малую окрестность u0. Поэтому полученное неравенство  противоречит предположению о том, что u0 — точка локального минимума (первая часть теоремы доказана).
противоречит предположению о том, что u0 — точка локального минимума (первая часть теоремы доказана).
Пусть u(1), u(2) — две различные точки глобального минимума. Из строгой выпуклости 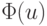 следует, что для всех
следует, что для всех ![\alpha \in \left[{0,1}\right]](/sites/default/files/tex_cache/1177db47a57889c7fb3191c37641e354.png) выполняется строгое неравенство
выполняется строгое неравенство ![\Phi \left[{\alpha u^{(1)} + (1 - \alpha )u^{(2)}}\right] < \alpha \Phi (u^{(1)}) + (1 - \alpha )\Phi (u^{(2)}) =\\
= \Phi * = \min\limits_U\Phi (u),](/sites/default/files/tex_cache/667a017d7850339d390729761b299351.png) что противоречит предположению о
том, что u(1), u(2) — точки глобального минимума.
что противоречит предположению о
том, что u(1), u(2) — точки глобального минимума.