НОУ ИНТУИТ | Численные методы решения уравнений в частных производных. Лекция 4: Введение в методы численного решения уравнений газовой динамики

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

|

Вам нравится? Нравится 20 студентам

| Поделиться |

Поддержать программу

4.5. Метод частиц в ячейках Харлоу (PIC method:Particle - In - Cell)

Метод PIC разработан Харлоу в Лос - Аламосской лаборатории (США) в 60 - х годах прошлого века для расчета процессов с большими деформациями исходной области интегрирования (расплескивание, разрушение).

Область интегрирования покрывается фиксированной в пространстве расчетной сеткой, шаг которой h постоянен по обеим координатам x, y, ячейки занумерованы двумя индексами k, l.

В центре ячейки вычисляются величины 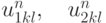$u_{1kl}^{n}, \quad u_{2kl}^{n}$ (компоненты скорости газа), 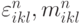$\varepsilon_{ikl}^{n}, m_{ikl}^{n}$ где i — номер вещества. 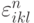$\varepsilon_{ikl}^{n}$ — удельная внутренняя энергия газа с номером i, 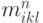$m_{ikl}^{n}$ — масса этого вещества. Если этого вещества в ячейке нет, то в ней и энергия, и масса полагаются равными нулю.

Предположим, что в каждой ячейке содержится несколько частиц (5 - 10), каждая из которых характеризуется координатами 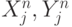$X_j^{n}, Y_j^{n}$ массой 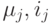$\mu _{j}, i_{j}$ — номер вещества, из которого состоит частица с номером j.

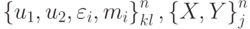Шаг численного интегрирования состоит в расчете величин $\left\{u_1, u_2, \varepsilon_i, m_i\right\}_{kl}^{n + 1}$ и $\left\{{X, Y}\right\}_j^{n + 1}$ на верхнем временном слое t_{n + 1} по вычисленным величинам $\left\{u_1, u_2, \varepsilon_i, m_i\right\}_{kl}^{n}, \left\{{X, Y}\right\}_j^{n}$ на нижнем слое t_n.

На первом этапе расчета учитываются изменения искомых функций только за счет сил давления. При этом предположении разностные соотношения аппроксимируют уравнения

$\begin{gather*} \frac{{{\partial}{\rho}}}{{\partial}t} = 0, \\ \frac{{{\partial}({\rho}u_1 )}}{{\partial}t} = - \frac{{\partial}p}{{\partial}x}, \\ \frac{{{\partial}({\rho}u_2 )}}{{\partial}t} = - \frac{{\partial}p}{{\partial}y}, \\ \frac{{{\partial}E}}{{\partial}t} + \frac{{{\partial}(pu_1 )}}{{\partial}x} + \frac{{{\partial}(pu_2 )}}{{\partial}y} = 0, \end{gather*}$

где

$E = {\rho}e = {\rho}\left[{\varepsilon + \frac{1}{2}(u_1^2 + u_2^2 )}\right].$

В расчетах участвуют также уравнения состояния для каждого газа

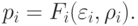
$p_{i} = F_{i}(\varepsilon _{i}, \rho _{i}).$

На втором этапе аппроксимируются конвективные члены

$\begin{gather*} \frac{{\partial}{\rho}}{{\partial}t} + \frac{{\partial}({\rho}u_1)}{{\partial}x} + \frac{{\partial}({\rho}u_2 )}{{\partial}y} = 0, \\ \frac{{\partial}{\rho}}{{\partial}t} + \frac{{\partial}({\rho}u_1)}{{\partial}x} + \frac{{\partial}({\rho}u_2 )}{{\partial}y} = 0, \\ \frac{{\partial}({\rho}u_1 )}{{\partial}t} + \frac{{\partial}({\rho}u_1^2 )}{{\partial}x} + \frac{{\partial}({\rho}u_1 u_2)}{{\partial}y} = 0, \\ \frac{{\partial}({\rho}u_2)}{{\partial}t} + \frac{{\partial}({\rho}u_1u_2)}{{\partial}x} + \frac{{\partial}({\rho}u_2)}{{\partial}y} = 0, \\ \frac{{\partial}E}{{\partial}t} + \frac{{\partial}(Eu_1)}{{\partial}x} + \frac{{\partial}(Eu_2)}{{\partial}y} = 0. \end{gather*}$

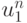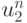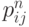Опишем вычислительную процедуру на первом этапе. Известны $u_1^{n}$ , $u_2^{n}$ , mⁿ, $\varepsilon ^{n}$ , Xⁿ, Yⁿ (остальные индексы для простоты изложения опускаются). Сначала рассчитывается давление $p_{ij}^{n}$ , исходя из предложения равенства давлений на границе двух сред p₁ = p₂ = ..., или

$F_1 (\varepsilon_1^{n}, \gamma_1^{- 1} m_1^{n} ) = F_2 (\varepsilon_2^{n}, \gamma_2^{- 1}m_2^{n} ) = \ldots$

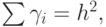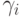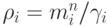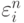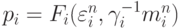К этим уравнениям добавляется условие $\sum {\gamma_i = h^2, }$ поскольку $\gamma _{i}$ — часть объема h² ячейки, занимаемого газом с номером i. По известной массе i газа находим его плотность: $\rho_i = m_i^{n}/{\gamma}_i$ , а по известной удельной энергии $\varepsilon_i^{n}$ - давление $p_i = F_i (\varepsilon_i^{n}, \gamma_i^{- 1} m_i^{n})$ .

Затем по закону Дальтона находится давление, 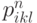$p_{ikl}^{n}$ , которое приписывается к центру ячейки k, l. Система нелинейных алгебраических уравнений решается, вообще говоря, итерационным методом. В случае 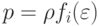$p = \rho f_{i}(\varepsilon )$ выписывается ее явное решение. Далее находим предварительные значения расчитываемых величин, которые обозначим как 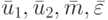$\bar{u}_1 , \bar{u}_2 , \bar{m}, \bar{\varepsilon}$ . Первое из уравнений

$\frac{{{\partial}\rho }}{{\partial}t} = 0$

закон сохранения массы — на сетке приобретает вид $\bar{m}_{ikl} = m_{ikl}^{n}$ . Поскольку на первом этапе

$\frac{{\partial}{\rho}}{{\partial}t} = 0$

, то два следующих разностных уравнения — уравнения движения — записываются как

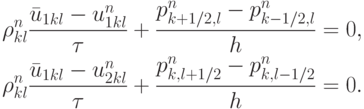
$\begin{gather*} \rho_{kl}^{n} \frac{{\bar{u}_{1{kl}} - u_{1{kl}}^{n}}}{\tau} + \frac{{p_{k + 1/2, l}^{n} - p_{k - 1/2, l}^{n}}}{h} = 0, \\ \rho_{kl}^{n} \frac{{\bar{u}_{1{kl}} - u_{2{kl}}^{n}}}{\tau} + \frac{{p_{{k, l} + 1/2}^{n} - p_{{k, l} - 1/2}^{n}}}{h} = 0. \end{gather*}$

Здесь

$\begin{gather*} p_{k + 1/2, l}^{n} = \frac{1}{2}(p_{kl}^{n} + p_{k + 1, l}^{n} ), \\ m_{kl}^{n} = \sum\limits_i {m_{ikl}^{n}}, \rho_{kl}^{n} = m_{kl}^{n}/h^2 . \end{gather*}$

Последняя из рассчитываемых величин — энергия. Дискретный аналог уравнения энергии в методе частиц в ячейках будет

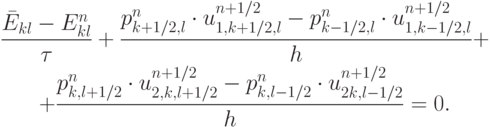
$\begin{gather*} \frac{{\bar{E}_{kl} - E_{kl}^{n}}}{\tau} + \frac{{p_{k + 1/2, l}^{n} \cdot u_{1 , k + 1/2, l}^{{n} + 1/2} - p_{k - 1/2, l}^{n} \cdot u_{1 , k - 1/2, l}^{{n} + 1/2}}}{h} + \\ + \frac{{p_{{k, l} + 1/2}^{n} \cdot u_{2 , {k, l} + 1/2}^{{n} + 1/2} - p_{{k, l} - 1/2}^{n} \cdot u_{2{k, l} - 1/2}^{{n} + 1/2}}}{h} = 0. \end{gather*}$

Здесь

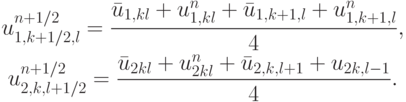
$\begin{gather*} u_{1, k + 1/2, l}^{{n} + 1/2} = \frac{{\bar{u}_{1, {kl}} + u_{1, {kl}}^{n} + \bar{u}_{1, k + 1, l} + u_{1 , k + 1, l}^{n}}}{4}, \\ u_{2 , {k, l} + 1/2}^{{n} + 1/2} = \frac{{\bar{u}_{2 {kl}} + u_{2 {kl}}^{n} + \bar{u}_{2, {k, l} + 1} + u_{2 {k, l} - 1}}}{4}. \end{gather*}$

Вычислим величину $e_{kl}^{n}$ — энергию. Напомним, что

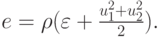
$e = {\rho}(\varepsilon + \frac{{u_1^2 + u_{2}^{2}}}{2}).$

Тогда eh² есть энергия в ячейке h x h:

${\rm E}_{kl}^{n} \cdot h^2 = \left[{(h^2 \cdot {\rho}) \cdot \varepsilon + (h^2 {\rho}) \frac{{u_1^2 + u_2^2}}{2}}\right]_{kl}^{n},$

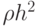где $\rho h^{2}$ — масса ячейки, равная 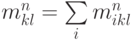$m_{kl}^{n} = \sum\limits_i {m_{ikl}^{n} }$ . В таком случае, с учетом закона сохранения массы,

$\left[{(h^2 {\rho}) \frac{{u_1^2 + u_2^2}}{2}}\right]_{kl}^{n} = \frac{1}{2}m_{kl}^{n} \left[{(u_{1, {kl}}^{n} )^2 + (u_{2 , {kl}}^{n} )^2}\right].$

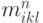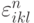Вычислим величину $\left[{(h^2 {\rho}) \varepsilon }\right]_{kl}^{n}$ , имеющую смысл полной внутренней энергии в ячейке, зная массу $m_{ikl}^{n}$ и удельную внутреннюю энергию $\varepsilon_{ikl}^{n}$ вещества.