| Россия |
Введение в методы численного решения уравнений газовой динамики
4.4. Разностная схема И.М. Гельфанда для численного решения одномерной системы уравнений газовой динамики
Система уравнений газодинамики решается в области 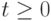 ,
, ![\eta \in \left[{0, X}\right]](/sites/default/files/tex_cache/d899055a10e2e5701af774ebf5377283.png) , отрезок интегрирования разбивается на интервалы узлами
, отрезок интегрирования разбивается на интервалы узлами 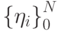 . Все интервалы заполнены
газом, что соответствует приближению механики сплошной среды. Величины на интервалах считаются кусочно - постоянными. При численном решении определяются шесть функций:
. Все интервалы заполнены
газом, что соответствует приближению механики сплошной среды. Величины на интервалах считаются кусочно - постоянными. При численном решении определяются шесть функций: 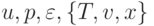 — скорость, давление, удельная внутренняя энергия, температура, удельный объем, эйлерова координата.
— скорость, давление, удельная внутренняя энергия, температура, удельный объем, эйлерова координата.
Для решения задачи используется система одномерных нестационарных уравнений
в частных производных, описывающих поведение газа в лагранжевых переменных (  — лагранжева координата):
— лагранжева координата):
![\begin{gather*}
\frac{{dv}}{dt} - \frac{du}{{{\partial}\eta }} = 0, \\
\frac{du}{dt} + \frac{{{\partial}(p + Q)}}{{{\partial}\eta }} = 0, \\
\frac{d}{dt} \left({\varepsilon + \frac{{u^2}}{2}}\right) + \frac{{{\partial}\left[{(p + Q)u}\right]}}{{{\partial}\eta }} = \frac{{\partial}}{{{\partial}\eta }} \left[{a({T, v}) \frac{{\partial}t}{{{\partial}\eta }}}\right], \\
\frac{dx}{dt} = u.
\end{gather*}](/sites/default/files/tex_cache/7aeea92c4ef1fc4793f1013d8a9a71b8.png) |
( 4.5) |
Здесь a(T, v) — заданный коэффициент теплопроводности,
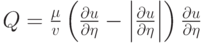
- искусственная вязкость Рихтмайера - Неймана,  —
коэффициент искусственной вязкости. Очевидно, что
—
коэффициент искусственной вязкости. Очевидно, что  если
если
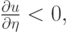
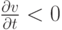
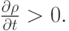
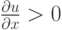
Коэффициент теплопроводности зависит от температуры и задается как

Начальные данные для рассматриваемой задачи будут
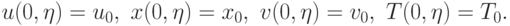
Условия на границах выбираем следующие:
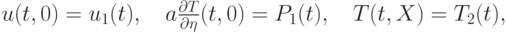
При численном интегрировании полагаем, что значения функций { u, T,
, v, x }известны на n слое и задача состоит в вычислении этих же функций на n + 1 слое. Сеточные функции { 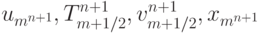 } вычисляются с помощью
неявной разностной схемы.
} вычисляются с помощью
неявной разностной схемы.
В результате разностная схема записывается как
![\begin{gather*}
\frac{{{{v}}_{m + 1/2}^{n + 1} - {{v}}_{m + 1/2}^{n}}}{\tau} - \frac{{u_{m + 1}^{n + 1} - u_m^{n + 1}}}{2} = 0, m = 1, \ldots , M, \\
\frac{u_m^{n + 1} - u_m^{n}}{\tau} + \frac{{(p + Q)}_{m + 1/2}^{n + 1} - {(p + Q)}_{m - 1/2}^{n + 1}}{h_m} = 0 \\
{h_m = \eta_{m + 1/2} - \eta_{m - 1/2}, m = 1, \ldots , M - 1, } \\
\frac{1}{\tau} \left[{\varepsilon_{m + 1/2}^{n + 1} + \frac{{(u_m^{n + 1})^2 +
(u_{m + 1}^{n + 1} )^2}}{4} - \varepsilon_{m + 1/2}^{n} - \frac{{(u_m^{n} )^2 + (u_{m + 1}^{n} )^2}}{4}}\right] + \\
+ \frac{1}{{h_{m + 1/2}}} \left[{(p + Q)_{m + 1}^{n + 1}u_{m + 1}^{n + 1} - (p + Q)_m^{n + 1}u_m^{n + 1}}\right] = \\
= \frac{1}{{h_{m + 1/2}}} \left[{a_{m + 1} \frac{{T_{m + 3/2}^{n + 1} - T_{m + 1/2}^{n + 1}}}{{h_{m + 1}}} - a_m \frac{{T_{m + 1/2}^{n + 1} - T_{m - 1/2}^{n + 1}}}{{h_m }}}\right], \\
h_{m + 1/2} = \eta_{m + 1} - \eta_m , m = 1, \ldots , M - 1, \\
\frac{x_m^{n + 1} - x_m^{n}}{\tau} - \frac{u_m^{n + 1} - u_m^{n}}{2} = 0, \quad
m = 0, \ldots , M. \end{gather*}](/sites/default/files/tex_cache/08a2b535e0ab2e028f3837b2710755e8.png) |
( 4.6) |
К этим уравнениям системы добавим разностное выражение для вычисления искусственной вязкости
 $](/sites/default/files/tex_cache/aa1cc252f6ef1df88563bc62b4825953.png)
с фиктивным краевым условием QM + 1/2 = 0 и интерполяционное выражение для pm
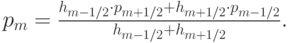
Схема имеет второй порядок аппроксимации по координате, а при весовом коэффициенте, равном 0, 5, и второй порядок по времени, причем все точки спектра лежат на единичной окружности. Подробнее о данной схеме в [14.10].
