Численные методы решения уравнений в частных производных

:

Численные методы решения уравнений в частных производных
[+]
Опубликован: 25.10.2007 | Уровень: профессионал | Доступ: платный
Лекция 4:

Введение в методы численного решения уравнений газовой динамики
A
|
версия для печати
< Лекция 3 || Лекция 4: 123456 || Лекция 5 >

4.2. Методы Лакса - Вендроффа и Мак - Кормака

Если система уравнений газодинамики записана в дивергентной форме

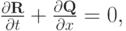
$ \frac{{{\partial}{\mathbf{R}}}}{{\partial}t} + \frac{{{\partial}{\mathbf{Q}}}}{{\partial}x} = 0, $

то запись разностных схем, соответствующих методам Лакса - Вендроффа и Мак - Кормака, аналогична их записи для численного решения уравнения переноса ( "Численные методы решения уравнений в частных производных гиперболического типа (на примере уравнения переноса)" ).

Так, схема Лакса - Вендроффа может быть представлена в следующем виде:

\begin{gather*} \frac{\mathbf{\tilde{R}}_{m + 1/2} - 0.5(\mathbf{R}_{m + 1}^n + \mathbf{R}_m^n)}{\tau/2} + \frac{\mathbf{Q}_{m + 1}^n - \mathbf{Q}_m^n}{h} = 0, \\ \frac{\mathbf{\tilde{R}}_{m - 1/2} - 0.5(\mathbf{R}_m^n + \mathbf{R}_{m - 1}^n)} {\tau /2} + \frac{\mathbf{Q}_m^n - \mathbf{Q}_{m - 1}^n}{h} = 0. \end{gather*}

(первый этап);

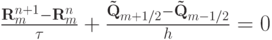
$ \frac{{{\mathbf{R}}_m^{n + 1} - {\mathbf{R}}_m^{n}}}{\tau} + \frac{{{\mathbf{\tilde{Q}}}_{m + 1/2} - {\mathbf{\tilde{Q}}}_{m - 1/2}}}{h} = 0 $

(второй этап).

Схему МакКормака представим следующим образом:

\begin{gather*} \frac{\mathbf{\tilde{R}}_m - \mathbf{R}_m^n}{\tau} + \frac{\mathbf{Q}_{m + 1} - \mathbf{Q}_m}{h} = 0, \\ \frac{\mathbf{\tilde{R}}_{m - 1} - \mathbf{R}_{m - 1}^n}{\tau} + \frac{\mathbf{Q}_m - \mathbf{Q}_{m - 1}}{h} = 0 \end{gather*}

(первый этап);

$ \frac{{{\mathbf{R}}_m^{n + 1} - 0.5({\mathbf{R}}_m^{n} + {\mathbf{\tilde{R}}}_m )}}{\tau} + \frac{{{\mathbf{\tilde{Q}}}_m - {\mathbf{\tilde{Q}}}_{m - 1}}}{{2h}} = 0 $

(второй этап).

Так как использована дивергентная форма записи исходных уравнений, то можно ожидать, что полученные таким образом схемы окажутся консервативными. О консервативных схемах газовой динамики подробнее в [14.4], [14.5].

4.3. Сеточно - характеристический метод для численного решения уравнений газовой динамики (М. - К.М.Магомедова - А.С.Холодова)

Этот метод (точнее, семейство методов) наиболее эффективен при численном решении задач, для которых существенным являются учет волновых процессов в сплошной среде. Подробнее о методе в книге [14.6], детальное описание — в монографии [14.7].

Матрица \mathbf{A} системы уравнений газовой динамики, записанной в форме

\begin{gather*} \frac{{\partial}\mathbf{U}}{{\partial}t} + \mathbf{A} \frac{{\partial}\mathbf{U}}{{\partial}x} + \mathbf{f} = 0, \\ \mathbf{U} = (\rho, u, \varepsilon)^T, \mathbf{A} = \left( \begin{array}{ccc} {u} & {\rho} & 0 \\ {\frac{1}{\rho} \frac{{\partial}p}{{\partial}\rho}} & {u} & {\frac{1} {\rho} \frac{{\partial}p}{{\partial}\varepsilon}} \\ 0 & {p/ \rho} & {u} \\ \end{array} \right), \end{gather*}

имеет вещественные собственные числа 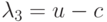\lambda _{1} = u + c, \lambda _{2} = u, \lambda _{3} = u - c и соответствующие им собственные векторы, \Omega _{i} (например, левые, которые находятся при решении системы линейных алгебраических уравнений {\omega }_{i}{\mathbf{A}} = \lambda_i {\omega }_i ). Таким образом, одномерная система уравнений газовой динамики является квазилинейной системой гиперболического типа.

Матрица из левых собственных векторов, записанных в строку, является матрицей перехода в базис из собственных векторов матрицы \mathbf{A}:

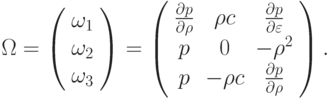
$ \Omega = \left( \begin{array}{l} {{\omega }_1} \\ {{\omega }_2} \\ {{\omega }_3 } \\ \end{array} \right) = \left( \begin{array}{ccc} {\frac{{\partial}p}{{{\partial}{\rho}}}} & {{\rho}c} & {\frac{{\partial}p} {{{\partial}\varepsilon }}} \\ p & 0 & {- {\rho}^2} \\ p & {- {\rho}c} & {\frac{{\partial}p}{{{\partial}{\rho}}}} \\ \end{array} \right). $

Матрица \mathbf{A} представима в виде \mathbf{A} = \mathbf{\Omega}^{- 1}\mathbf{{\Lambda}\Omega}, где \Lambda — диагональная матрица, состоящая из собственных чисел матрицы \mathbf{A}:

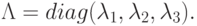
\Lambda = diag(\lambda _{1}, \lambda _{2}, \lambda _{3}).

Для получения разностной схемы введем обозначения

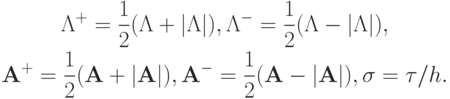
\begin{gather*} {\Lambda}^{+} = \frac{1}{2}({{\Lambda}} + \left|{{\Lambda}}\right|), {\Lambda}^{-} = \frac{1}{2}({{\Lambda}} - \left| {{\Lambda}}\right|), \\ {\mathbf{A}}^{+}= \frac{1}{2}({\mathbf{A}} + \left| {\mathbf{A}}\right|), {\mathbf{A}}^{-} = \frac{1}{2}({\mathbf{A}} - \left| {\mathbf{A}}\right|), {\sigma}= \tau/h. \end{gather*}

Рис. 4.1.

Умножим каждое из уравнений исходной системы газодинамики, записанных в матричной форме на 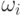\mathbf{\omega}_i ; в результате получим

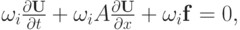
$ {\omega }_i \frac{{{\partial}{\mathbf{U}}}}{{\partial}t} + {\omega }_i A \frac{{{\partial}{\mathbf{U}}}}{{\partial}x} + {\omega }_i {\mathbf{f}} = 0, $

или, учитывая, что 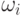\omega _{i} — левый собственный вектор,

$ {\omega }_i \frac{{{\partial}{\mathbf{U}}}}{{\partial}t} + (\lambda_i {\omega }_i ) \frac{{{\partial}{\mathbf{U}}}}{{\partial}x} + {\omega }_i {\mathbf{f}} = 0. $

Построим разностную аппроксимацию полученной системы уравнений в частных производных с учетом знака собственных чисел (или направления характеристик). Для облегчения восприятия ограничимся простейшим методом первого порядка аппроксимации

$ {\omega }_i \frac{{{\mathbf{U}}_m^{n + 1} - {\mathbf{U}}_m^{n}}}{\tau} \mp \lambda_i{\omega }_i \frac{{{\mathbf{U}}_{m \mp 1}^{n} - {\mathbf{U}}_m^{n}}}{h} + {\omega }_i {\mathbf{f}} = 0. $

Приведенное выше разностное уравнение может быть записано в матричной форме

\begin{gather*} {\Omega }({\mathbf{U}}_m^{n + 1} - {\mathbf{U}}_m^{n} ) - {\sigma}{{\Lambda}}^{+} {\Omega }({\mathbf{U}}_{m - 1}^{n} - {\mathbf{U}}_m^{n} ) + \\ + {\sigma}{{\Lambda}}^{-}{\Omega }({\mathbf{U}}_{m + 1}^{{n}} - {\mathbf{U}}_m^{n} ) + {\tau}{\Omega \mathbf{f}}_m^{n} = 0, \end{gather*}

или в виде, разрешенном относительно верхнего слоя:

\begin{gather*} {\mathbf{U}}_m^{n + 1} = {\mathbf{U}}_m^{n} - \sigma \left[({\Omega }^{- 1}{{\Lambda}}^{+} {\Omega })_m^{n}({\mathbf{U}}_{m - 1}^{n} - {\mathbf{U}}_m^{n} ) -\right. \\ \left. - ({\Omega }^{- 1}{{\Lambda}}^{-} {\Omega })_m^{n} ({\mathbf{U}}_{m + 1}^{n} - {\mathbf{U}}_m^{n} )\right] + {\tau}{\mathbf{f}}_m^{n}, \end{gather*}

или в компактной форме:

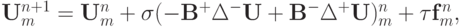
{\mathbf{U}}_m^{n + 1} = {\mathbf{U}}_m^{n} + {\sigma}(- {\mathbf{B}}^{+} {\Delta}^{-}{\mathbf{U}} + {\mathbf{B}}^{-}{\Delta}^{+}{\mathbf{U}})_m^{n} + {\tau}{\mathbf{f}}_m^{n},

где

{\mathbf{B}}^{+} = {{\Omega}}^{- 1}{{\Lambda}}^{+}{{\Omega }}, {\mathbf{B}}^{-} = {\Omega }^{- 1}{{\Lambda}}^{-} {{\Omega}}.

Учет направления характеристик позволяет получать устойчивые разностные схемы для системы уравнений газовой динамики. Сеточно - характеристические схемы позволяют гибко менять форму шаблона в зависимости от локальных свойств решения задачи. Существует обобщение методов на случаи двух и трех пространственных измерений. В сочетании с методом неопределенных коэффициентов сеточно - характеристические схемы дали очень хорошие результаты не только в традиционной газовой динамике, но и в механике деформируемого твердого тела, магнитной гидродинамике [14.6], [14.7].

Дальше >>
< Лекция 3 || Лекция 4: 123456 || Лекция 5 >

Вопросы и ответы

вопросов: 0

Студенты

всего: 30
Максим Радунцев
Максим Радунцев
Россия
предложить дружбу
Надежда Павленко
Надежда Павленко
Россия, Ставрополь
предложить дружбу