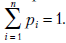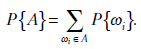|
В дисциплине "Основы эконометрики" тест 6 дается по теме 7. |
Приложение 2: Основные положения теории вероятностей
В теории вероятностей понятие события является первичным и не определяется через другие более простые понятия. Для описания событий как результатов испытаний (опыта или наблюдения) с неопределенным исходом используется понятие случайности. Под испытанием (экспериментом) понимают любое наблюдение какого-либо явления, которое выполнено в заданном комплексе условий с фиксацией результата и может быть повторено в принципе достаточное число раз.
Испытание, исход которого не может быть определен однозначно до проведения эксперимента, принято называть случайным.
Наряду с событием  в рассмотрение вводится противоположное событие
в рассмотрение вводится противоположное событие  , которое заключается в том, что событие
, которое заключается в том, что событие  не происходит.
не происходит.
Событие, которое при случайном испытании происходит всегда, называется достоверным и обозначается  .
.
Событие, которое никогда не происходит, т.е. является противоположным достоверному, называется невозможным и обозначается  .
.
События  и
и  называются несовместными, если появление одного из них исключает появление другого. Другими словами, такие события никогда не происходят одновременно.
называются несовместными, если появление одного из них исключает появление другого. Другими словами, такие события никогда не происходят одновременно.
Предполагается, что на рассматриваемом множестве событий могут быть определены:
-
сумма событий
 и
и  (обозначается
(обозначается  ) - событие C, состоящее в том, что произойдет хотя бы одно из событий
) - событие C, состоящее в том, что произойдет хотя бы одно из событий  и
и  ;
; -
произведение событий
 и
и  (обозначается
(обозначается 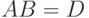 ) - событие
) - событие  , состоящее в том, что произойдут оба события
, состоящее в том, что произойдут оба события  и
и  .
.
Событие эксперимента (испытания) считается элементарным, если его нельзя представить с помощью определенных выше операций, через другие события.
Совокупность всех таких событий 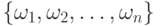 образует пространство элементарных исходов.При этом выполняются соотношения
образует пространство элементарных исходов.При этом выполняются соотношения
Предполагается, что каждому исходу 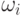 , возможному в данном случайном испытании, может быть приписана некоторым образом неотрицательная числовая функция
, возможному в данном случайном испытании, может быть приписана некоторым образом неотрицательная числовая функция  , такая что
, такая что
Значения этой функции, выражающие меру возможности осуществления элементарного события  , называются его вероятностью. При этом имеют место следующие свойства вероятности:
, называются его вероятностью. При этом имеют место следующие свойства вероятности:  . В рамках такого подхода любое событие
. В рамках такого подхода любое событие  , связанное с этим экспериментом, определяется как сумма элементарных исходов, а его вероятность как сумма вероятностей соответствующих элементарных исходов:
, связанное с этим экспериментом, определяется как сумма элементарных исходов, а его вероятность как сумма вероятностей соответствующих элементарных исходов:
Для введенных таким образом понятий событий и их вероятностей справедливы следующие два утверждения, носящих названия теорем:
-
 , если
, если  , - теорема сложения вероятностей для несовместных событий;
, - теорема сложения вероятностей для несовместных событий; -
 , если
, если  , - теорема сложения вероятностей для совместных событий.
, - теорема сложения вероятностей для совместных событий.
Условная вероятность и независимость событий
Если некоторое событие  рассматривается не на всем пространстве элементарных исходов, а лишь на некоторой его части, где осуществляется другое событие
рассматривается не на всем пространстве элементарных исходов, а лишь на некоторой его части, где осуществляется другое событие  , то имеет смысл перейти к рассмотрению условной вероятности события
, то имеет смысл перейти к рассмотрению условной вероятности события  , которая определяется следующим образом:
, которая определяется следующим образом:
Из этого определения непосредственно следует теорема умножения вероятностей:

Полагают, что событие  не зависит от события
не зависит от события  , если
, если 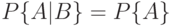 . Другими словами, события
. Другими словами, события  и
и  считаются
считаются , если появление одного из них не изменяет вероятности другого события. Для независимых событий теорема умножения вероятностей принимает вид
, если появление одного из них не изменяет вероятности другого события. Для независимых событий теорема умножения вероятностей принимает вид

Обычно последнее равенство в более общих случаях рассматривают в качестве определения независимости событий  и
и  .
.
Независимость случайных событий является очень важным понятием для эконометрических моделей. Достаточно отметить, что многие свойства статистических оценок получаются именно в предположении независимости входящих в них случайных величин. А понятие условной вероятности используется при определении регрессионной модели.