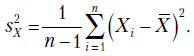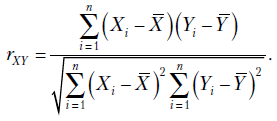|
В дисциплине "Основы эконометрики" тест 6 дается по теме 7. |
Приложение 2: Основные положения теории вероятностей
Основные понятия математической статистики. Точечные оценки параметров
В математической статистике исследуемую случайную величину, в общем случае - многомерную, принято называть генеральной совокупностью, а ее реализации в последовательности независимых испытаний - выборкой из генеральной совокупности, или коротко - выборкой. Сами значения случайной величины принято называть элементами выборки, а их количество - объемом выборки. Основной задачей статистического исследования является описание генеральной совокупности по имеющейся выборке. Как правило, эта задача сводится к нахождению закона распределения случайной величины  или определению ее числовых характеристик.
или определению ее числовых характеристик.
Статистикой называется любая функция элементов выборки 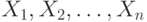 . Если рассматривать элементы выборки как независимые одинаково распределенные случайные величины, то и статистику следует рассматривать как случайную величину, имеющую свой закон распределения.
. Если рассматривать элементы выборки как независимые одинаково распределенные случайные величины, то и статистику следует рассматривать как случайную величину, имеющую свой закон распределения.
Любые характеристики случайной величины, полученные по выборке, называются выборочными, или эмпирическими. Статистической оценкой называется выборочная характеристика, используемая в качестве приближенного значения неизвестной характеристики генеральной совокупности. Так, статистической оценкой плотности распределения непрерывной случайной величины является гистограмма.
Статистическая оценка, представленная в виде числа - точки на числовой прямой, называется точечной. Пригодность использования в приложениях точечной оценки зависит от наличия у нее таких свойств, как несмещенность, состоятельность и эффективность.
Пусть 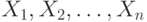 - случайная выборка и
- случайная выборка и  — выборочная оценка некоторого параметра
— выборочная оценка некоторого параметра  . Оценка
. Оценка 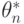 называется несмещенной, если для любого фиксированного
называется несмещенной, если для любого фиксированного  выполняется равенство
выполняется равенство 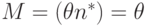 . Это равенство гарантирует, что использование этой оценки не приводит к систематическим ошибкам.
. Это равенство гарантирует, что использование этой оценки не приводит к систематическим ошибкам.
Оценка 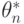 называется состоятельной, если она сходится по вероятности к значению параметра
называется состоятельной, если она сходится по вероятности к значению параметра  , т.е. выполняется условие
, т.е. выполняется условие 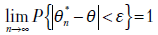 для любого
для любого 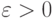 . Выполнение этого условия означает, что с увеличением объема выборки возрастает наша уверенность в малом по абсолютной величине отклонении оценки
. Выполнение этого условия означает, что с увеличением объема выборки возрастает наша уверенность в малом по абсолютной величине отклонении оценки 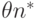 от истинного значения параметра
от истинного значения параметра  .
.
Оценка 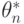 считается эффективной, если она обладает наименьшей дисперсией по сравнению с любыми другими оценками. Эффективная оценка является наилучшей в смысле минимума среднеквадратичного отклонения оценки
считается эффективной, если она обладает наименьшей дисперсией по сравнению с любыми другими оценками. Эффективная оценка является наилучшей в смысле минимума среднеквадратичного отклонения оценки  от истинного значения параметра
от истинного значения параметра  .
.
В качестве оценки математического ожидания принято использовать среднее выборочное
Эта оценка является несмещенной, состоятельной, а в случае нормального распределения генеральной совокупности - эффективной.
Несмещенной, состоятельной оценкой дисперсии является выборочная (исправленная) дисперсия
Выборочная ковариация определяется формулой
где  и
и  — выборочные средние величин
— выборочные средние величин  и
и  соответственно;
соответственно;
величина 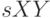 - выборочная оценка коэффициента ковариации
- выборочная оценка коэффициента ковариации 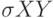 .
.
Оценкой коэффициента корреляции является выборочный коэффициент корреляции