|
В дисциплине "Основы эконометрики" тест 6 дается по теме 7. |
Приложение 3: Геометрическая интерпретация метода наименьших квадратов
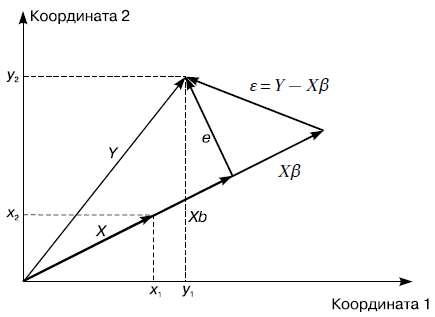
Для геометрического вывода условий, которым должны удовлетворять оценки коэффициентов  , рассмотрим частный случай исходных данных. Предположим, что имеются только два наблюдения, которые могут быть представлены в виде векторов
, рассмотрим частный случай исходных данных. Предположим, что имеются только два наблюдения, которые могут быть представлены в виде векторов  . Кроме того, будем предполагать, что прямая регрессионной модели проходит через начало координат, т.е. что
. Кроме того, будем предполагать, что прямая регрессионной модели проходит через начало координат, т.е. что  . Заметим, что это предположение не является сколько-нибудь существенным, поскольку для его выполнения достаточно центрирования исходных данных. В этом случае уравнению
. Заметим, что это предположение не является сколько-нибудь существенным, поскольку для его выполнения достаточно центрирования исходных данных. В этом случае уравнению 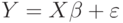 будут соответствовать следующие геометрические построения (рис.).
будут соответствовать следующие геометрические построения (рис.).
Вектор  (или
(или  ) получается путем умножения вектора
) получается путем умножения вектора  на число
на число  и, следовательно, будет коллинеарен вектору
и, следовательно, будет коллинеарен вектору  . Вектор
. Вектор  будет равняться разности векторов
будет равняться разности векторов  и
и  . Значение оценки вектора
. Значение оценки вектора  следует выбрать таким образом, чтобы модуль вектора
следует выбрать таким образом, чтобы модуль вектора  был минимальным. Как следует из геометрических построений, минимальное расстояние от точки с координатами
был минимальным. Как следует из геометрических построений, минимальное расстояние от точки с координатами  до прямой
до прямой  будет достигаться на перпендикуляре, опущенном из этой точки на указанную прямую. Следовательно, необходимым и достаточным условием минимизации
будет достигаться на перпендикуляре, опущенном из этой точки на указанную прямую. Следовательно, необходимым и достаточным условием минимизации 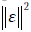 и 124 будет условие ортогональности
и 124 будет условие ортогональности  и
и  . Известно, что необходимым и достаточным условием ортогональности двух векторов является равенство нулю их скалярного произведения. Таким образом, получаем уравнение
. Известно, что необходимым и достаточным условием ортогональности двух векторов является равенство нулю их скалярного произведения. Таким образом, получаем уравнение  , которое называется нормальным. Выполнив соответствующие преобразования, приходим в общем случае к системе нормальных уравнений
, которое называется нормальным. Выполнив соответствующие преобразования, приходим в общем случае к системе нормальных уравнений

Если матрица системы  невырожденная, то существует обратная матрица
невырожденная, то существует обратная матрица  и система нормальных уравнений будет иметь решение
и система нормальных уравнений будет иметь решение

Оценки вектора  , полученные при решении системы нормальных уравнений, называются оценками, полученными по методу наименьших квадратов, или МНК-оценками. Зная значения решения
, полученные при решении системы нормальных уравнений, называются оценками, полученными по методу наименьших квадратов, или МНК-оценками. Зная значения решения  , можно вычислить расчетные (прогнозные) значения переменной
, можно вычислить расчетные (прогнозные) значения переменной  :
:

Геометрически вектор является ортогональной проекцией вектора  на линейное пространство, натянутое на векторы
на линейное пространство, натянутое на векторы 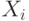 , т.е. наилучшей аппроксимацией
, т.е. наилучшей аппроксимацией  линейной комбинацией векторов
линейной комбинацией векторов 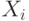 .
.
Из геометрических соображений также следует, что векторы  и
и  ортогональны, а следовательно, выполняется равенство
ортогональны, а следовательно, выполняется равенство

 .
.