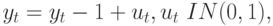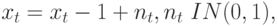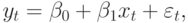|
В дисциплине "Основы эконометрики" тест 6 дается по теме 7. |
Ложная регрессия, коинтеграция и модели корректировки ошибок
12.1. Проблема обнаружения ложной корреляции в данных
Тренды в данных могут привести к ложным корреляциям, следствием которых являются ложные связи между переменными в регрессионном уравнении. Однако в действительности между собой коррелируют только временные тренды.
Временной тренд может быть исключен из результирующей переменной путем построения регрессии этой переменной по времени и перехода к остаткам, которые образуют новую стационарную переменную, уже свободную от тренда. Или этот тренд может быть сразу включен в модель путем введения времени в качестве одной из переменных-регрессоров. При этом используются регрессионные модели, основанные на стандартных  - и
- и  -тестах и оперирующие со стационарными временными рядами, имеющими постоянные средние и дисперсии.
-тестах и оперирующие со стационарными временными рядами, имеющими постоянные средние и дисперсии.
При построении регрессии нестационарной переменной на детерминированную переменную времени остатки обычно не дают в результате стационарную переменную.
Рассмотрим, например, два процесса случайного блуждания
где
 |
- | класс временных рядов с независимыми приращениями с нулевым средним и единичной дисперсией, подчиняющимися нормальному закону. |
Оба процесса представляют некоррелированные нестационарные переменные. Поэтому, если оценивается регрессионная модель
то естественно за нулевую гипотезу 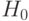 принять, что
принять, что 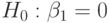 , и ожидать, что коэффициент детерминации
, и ожидать, что коэффициент детерминации 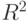 будет близок к нулю. Однако нестационарная природа данных влечет нестационарность
будет близок к нулю. Однако нестационарная природа данных влечет нестационарность 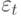 . Таким образом, любая тенденция к росту в обоих рядах ведет к появлению корреляции, которая и будет отражена в регрессионный модели. Хотя каждый ряд растет по совершенно разным причинам с некоррелированными уровнями роста, а значит, что в уравнении
. Таким образом, любая тенденция к росту в обоих рядах ведет к появлению корреляции, которая и будет отражена в регрессионный модели. Хотя каждый ряд растет по совершенно разным причинам с некоррелированными уровнями роста, а значит, что в уравнении 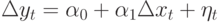 коэффициент
коэффициент 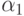 сходится по вероятности к нулю. Итак, корреляция между нестационарными рядами еще не означает наличие существенных (причинных) связей между ними, как это выводится в случае стационарных рядов.
сходится по вероятности к нулю. Итак, корреляция между нестационарными рядами еще не означает наличие существенных (причинных) связей между ними, как это выводится в случае стационарных рядов.
Кроме того, проблема ложной (кажущейся) корреляции, выражающаяся в ненулевой оценке коэффициента  , осложняется тем, что обычные выборочные
, осложняется тем, что обычные выборочные  - и
- и  -статистики не имеют стандартных распределений, как в случае стационарных рядов. Существует явная тенденция к отрицанию гипотезы
-статистики не имеют стандартных распределений, как в случае стационарных рядов. Существует явная тенденция к отрицанию гипотезы 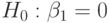 , которая возрастает по мере увеличения объема выборки. Были проведены по методу Монте-Карло следующие эксперименты. Уравнение (12.3) было оценено 10 000 раз, при этом
, которая возрастает по мере увеличения объема выборки. Были проведены по методу Монте-Карло следующие эксперименты. Уравнение (12.3) было оценено 10 000 раз, при этом  и
и 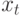 определялись по уравнениям (12.1) и (12.2). В результате оценок среднее значение
определялись по уравнениям (12.1) и (12.2). В результате оценок среднее значение 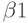 оказалось равным
оказалось равным 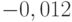 и соответствующая стандартная ошибка равна
и соответствующая стандартная ошибка равна 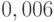 (при размере выборки
(при размере выборки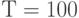 ). Это дает отрицание нулевой гипотезы. Основываясь на 10 000 повторений, вероятность отрицания
). Это дает отрицание нулевой гипотезы. Основываясь на 10 000 повторений, вероятность отрицания 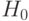 при уровне значимости 0,05 равна 0,753, т.е. для 75,3% регрессий были получены значения
при уровне значимости 0,05 равна 0,753, т.е. для 75,3% регрессий были получены значения  -статистики с
-статистики с  . Это объясняется тем, что средняя
. Это объясняется тем, что средняя  -статистика, полученная в эксперименте, равна -0,12 с соответствующим стандартным отклонением 7,3. Нестандартное распределение
-статистика, полученная в эксперименте, равна -0,12 с соответствующим стандартным отклонением 7,3. Нестандартное распределение  -статистики привело к очень высокой вероятности отрицания гипотезы
-статистики привело к очень высокой вероятности отрицания гипотезы 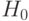 .
.
Это позволяет сделать вывод, что проблема ошибочного обнаружения связей часто возникает в не связанных между собой нестационарных временных рядах. Данная проблема возрастает с ростом выборки и не может быть разрешена путем выделения трендов в изучаемых рядах, как для стационарных рядов с временным трендом.
Возникает вопрос: когда можно делать вывод о причинной долговременной связи между нестационарными рядами, основываясь на регрессионном уравнении (12.3)? Решение этой проблемы лежит в области коинтеграции нестационарных временных рядов.
Говорят, что ряд содержит единичные корни и интегрируем с порядком  , т.е. принадлежит классу
, т.е. принадлежит классу 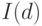 , если он становится стационарным после взятия
, если он становится стационарным после взятия  раз операций вычисления разности от временного ряда. В общем случае любая линейная комбинация рядов класса
раз операций вычисления разности от временного ряда. В общем случае любая линейная комбинация рядов класса 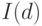 должна также принадлежать
должна также принадлежать 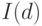 . Однако если существует такой вектор
. Однако если существует такой вектор  , при котором вектор возмущений
, при котором вектор возмущений 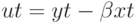 имеет меньший порядок интеграции
имеет меньший порядок интеграции 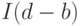 , где
, где  , то, по определению Р. Энгла и К. Грангера,
, то, по определению Р. Энгла и К. Грангера,  и
и 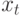 коинтегрированы с порядком
коинтегрированы с порядком  . Если
. Если 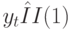 и
и 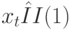 , а
, а  , то оба ряда коинтегрированы с порядком CI(1, 1).
, то оба ряда коинтегрированы с порядком CI(1, 1).
С экономической точки зрения, если два или более ряда коинтегрированы, то между ними существует равновесная устойчивая долговременная связь, хотя сами ряды содержат стохастические тренды, т.е. не стационарны. Концепция коинтеграции может быть интерпретирована как существование долговременного устойчивого равновесного соотношения между параметрами экономической системы, а 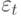 (см. (12.3)) - как расстояние (ошибка) от равновесного направления в пространстве состояний
(см. (12.3)) - как расстояние (ошибка) от равновесного направления в пространстве состояний  .
.