Ложная регрессия, коинтеграция и модели корректировки ошибок

12.2. Краткосрочные модели, коинтеграция и механизм корректировки ошибок

Даже если возможно прямо получить долгосрочную модель, имеет смысл рассмотреть краткосрочную эволюцию переменных при стремлении к долгосрочному состоянию. Это становится необходимым, если не удается обнаружить долгосрочные связи между переменными. В краткосрочных моделях можно использовать экономическую информацию, полученную в результате корректировки, регулирования процесса в целях улучшения прогноза в желаемом направлении.

Связи не всегда находятся в точке равновесия. Основная причина этого состоит в том, что экономические агенты не могут мгновенно приспособиться к новой информации. Часто текущее значение зависимой переменной определяется не только текущим значением объясняющей переменной , но и ее прошлыми значениями. В динамическую модель могут входить также прошлые значения самой зависимой переменной , что упрощает форму динамической модели. В противном случае в модель пришлось бы вводить большое число сильно коррелированных прошлых (с лагом) значений .

Одной из простых динамических краткосрочных моделей является уравнение

(12.4)

где

-

белый шум остатков, т.е. .

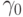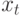Понятно, что параметр отражает краткосрочную реакцию на изменение , но не долгосрочный эффект, который присутствует в модели, находящейся в состоянии равновесия

(12.5)

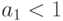Поэтому в долгосрочной модели эластичность между и равна в предположении, что . (Это условие необходимо, если краткосрочная модель сходится к долгосрочной.)

Динамическая модель (12.4) может быть легко усложнена (и часто она при этом становится более реалистичной), если увеличить число запаздываний по , т.е. параметр и число запаздываний по , а значит, параметр . Однако при работе с моделями такого вида возникает ряд трудностей. Прежде всего, как было отмечено, существует опасность высокой корреляции между текущими и прошлыми значениями переменных, которая создает проблему мультиколлинеарности (высокий 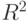, но неточная оценка параметров и малые значения -статистик в модели при том, что форма и число переменных в модели могут быть определены правильно).

Поэтому последовательное исключение незначащих переменных может привести к ошибочной спецификации модели, особенно в случае, когда - векторная переменная. Кроме того, многие, если не все, переменные, входящие в модель, могут быть нестационарными. Это ведет к потенциальной опасности ложной регрессии, так как в этом случае - и -статистики не подчинены стандартным распределениям и обычные выводы на их основе являются неверными.

Альтернативой может стать построение динамической модели в разностях. Правда, при этом теряется долгосрочная информация модели, что нежелательно при ее использовании в прогностических целях на долгий период.

Более удобным подходом представляется применение механизма корректировки ошибок динамической модели.

Преобразуем уравнение (12.4) к виду модели корректировки ошибок (МКО)

(12.6)

где

Уравнения (12.4) и (12.6) эквивалентны, но МКО (12.6) имеет несколько серьезных преимуществ. Во-первых, предполагая, что и коинтегрированы, она сочетает краткосрочный и долгосрочный эффекты. Это видно, когда при достижении долгосрочного равновесия уравнение (12.6) переходит в уравнение равновесия (12.5).

Итак, если в какой-то момент достигается равновесие, то

В течение неравновесного периода выражение в левой части последнего равенства ненулевое и измеряет расстояние от текущего положения системы до точки равновесия. Оценка параметра дает информацию о скорости контроля, т.е. о том, с какой скоростью проходит изменение в зависимости от расстояния до положения равновесия. Большие значения, близкие к 1, величины свидетельствуют о том, что экономические факторы (так как в модели участвуют обычно логарифмы натуральных выражений) сильно изменяют результат, если система далека от равновесия. Малые значения предполагают, что контроль и достижение долговременной стабилизации происходят медленно, возможно, ввиду высокой стоимости затрат на регулирование (в денежном и неденежном смысле). Предположим, что переменная начала увеличиваться не так быстро, как это заложено в уравнении (12.5), быть может, из-за большого отрицательного случайного колебания 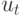. В этом случае 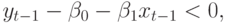так как растет медленнее . Но поскольку отрицательное, в результате произойдут увеличение и возврат по направлению к стабильному пути, определенному уравнением (12.5).

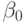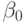Во-вторых, все члены в МКО стационарные, поэтому остается применимой стандартная регрессионная техника исследований, предполагающая проверку коинтеграции по критерию Дики - Фулера (в данном пособии не рассматриваются) и оценку коэффициентов и . Часто полагают единицей (полагают равным нулю) и идет проверка такой долговременной эластичности.

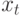В-третьих, МКО весьма близки к идее коинтеграции. Действительно, как показали Р. Энгл и Д. Грангер, если и коинтегрированы , тогда существует МКО, и наоборот, МКО генерирует коинтегрированные ряды. Практически результаты, полученные Энглом и Грангером, доказывают, что МКО обладают иммунитетом к ложной регрессии, благодаря тому, что хотя в уравнении присутствуют непреобразованные ряды, они коинтегрированы с некоторым стационарным рядом.

Отметим, что возможны обобщения и усложнения уравнения (12.6). В общем случае можно задать МКО в виде

(12.7)

где

	-	полиномиальный лаг-оператор ;
	-	полиномиальный лаг-оператор ;
	-	оператор запаздывания (лаг) и .

Наконец, есть возможность определить МКО в случае многих переменных, используя множество коинтегрированных векторов.

Контрольные вопросы

1. Объясните причины возникновения ложной корреляции, т.е. корреляции, не вызванной непосредственной связью между факторами, в нестационарном случае.
2. Как записать долгосрочную и краткосрочную модели связи между факторами?
3. Какие соотношения между временными рядами должны выполняться в случае их коинтеграции?
4. Как получить модели, учитывающие как долгосрочные связи между факторами, так и краткосрочные изменения временного ряда под воздействием случайных отклонений (модели корректировки ошибок - МКО)?
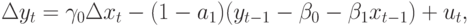
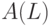
5. Исходя из чего можно предполагать, что в моделях корректировки ошибок, устанавливающих связи между коинтегрированными временными рядами, отсутствует ложная корреляция между факторами?