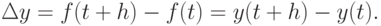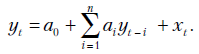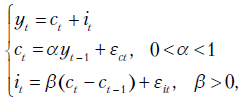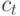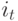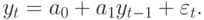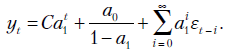НОУ ИНТУИТ | Введение в эконометрику. Лекция 9: Разностные уравнения и их решение

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 10.09.2016 | Уровень: для всех | Доступ: платный

|

Вам нравится? Нравится 27 студентам

| Поделиться |

Поддержать программу

Ключевые слова: функция, разность, ПО, запаздывания, коэффициенты, переменная, линейное уравнение, константы, значение, выражение, характеристическое уравнение, многочлен, линейная комбинация, частное решение, целое число, расходы, множитель, отношение

9.1. Уравнения первого и второго порядков

Пусть дана функция 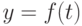y = f(t) . Тогда первая разность $\Delta$ y определяется по формуле

$\Delta y = f(t + h) - f(t) = y(t + h) - y(t).$

(9.1)

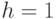В отличие от дифференциального исчисления мы не предполагаем, что стремится к нулю. Так как большинство экономических данных собираются через определенные равные промежутки времени, полезно считать, что h > 0 . Более того, обычно полагают период между наблюдениями нормализованным, т.е. выбирают h = 1 (один месяц, один квартал, один год). Поэтому первые разности можно записать в виде

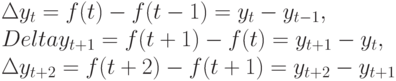
$\Delta y_{t} = f(t) - f(t - 1) = y_{t} - y_{t - 1},\\ Delta y_{t + 1} = f(t + 1) - f(t) = y_{t + 1} - y_{t},\\ \Delta y_{t + 2} = f(t + 2) - f(t + 1) = y_{t + 2} - y_{t + 1}$

и т.д.

Таким же образом сформируем вторую разность как изменение первой разности:

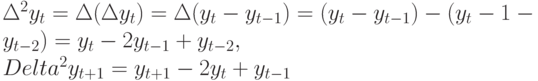
$\Delta ^{2}y_{t} = \Delta (\Delta y_{t}) = \Delta (y_{t} - y_{t - 1}) = (y_{t} - y_{t - 1}) - (y_{t} - 1 - y_{t - 2}) = y_{t} - 2y_{t - 1} + y_{t - 2},\\ Delta ^{2}y_{t + 1} = y_{t + 1} - 2y_{t} + y_{t - 1}$

и т.д.

Аналогично определяется разность n-го порядка:

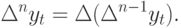
$\Delta ^{n}y_{t} = \Delta (\Delta ^{n-1}y_{t}).$

Так как в настоящем учебном пособии в основном рассматриваются линейные модели временных рядов, изучим только один специальный случай линейного разностного уравнения -го порядка с постоянными коэффициентами, а именно уравнение вида

(9.2)

Порядок разностного уравнения задается показателем - максимальной величиной шага запаздывания, или, другими словами, максимальным лагом. Уравнение считается линейным потому, что все значения зависимой переменной y входят в него в первой степени.

Коэффициенты 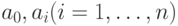$a_{0}, a_{i }(i = 1, \dots , n)$ называются параметрами уравнения и не зависят от значений и . Переменная представляет возмущающий процесс и может зависеть от времени, текущего и прошлого значений других переменных или иметь стохастический характер изменения. Соответственно, выбирая возмущающий процесс x, можно получить широкий спектр важных макроэкономических моделей.

Рассмотрим, например, стохастическую версию классической кейнсианской модели, предложенную Самуэльсоном:

(9.3)

где

$y_{t}$	-	реальный общий национальный продукт;
$c_{t}$	-	потребление;
$i_{t}$	-	инвестиции в момент времени .

Слагаемые 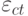$\varepsilon _{ct}$ и $\varepsilon _{it}$ имеют нулевые средние и объясняют случайные возмущения в потреблении и инвестировании.

Преобразуем кейнсианскую модель производства и потребления (9.3) к виду

$y_{t} = \alpha (1 + \beta )y_{t-1} - \alpha \beta by_{t-2} + (1 + \beta b)\varepsilon _{ct} + \varepsilon _{it} - \beta \varepsilon _{ct-1}.$

(9.4)

Уравнение (9.4) выражает $y_{t}$ как функцию от собственных запаздываний (лагов) и возмущающих членов. Выберем возмущающий процесс в виде

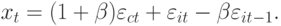
$x_{t} = (1 + \beta ) \varepsilon _{ct} + \varepsilon _{it} - \beta \varepsilon _{it}_{-1}.$

и получим разностное линейное уравнение второго порядка вида (9.2). Отметим, что в уравнении (9.4) отсутствует свободный член, т.е. 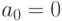$a_{0} = 0$ .

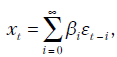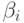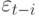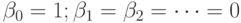Важный частный случай для последовательности {x_{t}} получаем при где $\beta_{i}$ - константы, $\varepsilon _{t-i}$ не зависят от . При этом можно полагать, что $\{\varepsilon _{t}\}$ является последовательностью неопределенных внешних (экзогенных) переменных. Например, если $\{\varepsilon _{t}\}$ - последовательность случайных ошибок наблюдений и $\beta _{0} = 1; \beta _{1} = \beta _{2} = \dots = 0$ , то уравнение (9.2) становится уравнением авторегрессии

$y_{t} = a_{0} + a_{1}y_{t - 1} +\dots + a_{n}y_{t} - n + \varepsilon _{t}.$

Пусть $n = 1, a_{0} = 0, a_{1} = 1$ . Тогда получаем модель случайного блуждания.

Другой полезный пример дает уравнение

$y_{t} = 0,7y_{t - 1} + \varepsilon _{t}.$

(9.5)

Можно проверить, что решением этого разностного уравнения первого порядка является функция

(9.6)

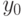Метод итераций (последовательных приближений). Обозначим известное значение функции в момент времени 0 как $y_{0}$ . Обратимся к разностному уравнению первого порядка

$y_{t} = a_{0} + a_{1}y_{t -1} + \varepsilon _{t}.$

(9.7)

Подставляя 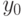$y_{0}$ в (9.7), получаем:

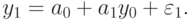
$y_{1} = a_{0} + a_{1}y_{0} + \varepsilon _{1}.$

Тем же путем находим 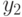$y_{2}$ :

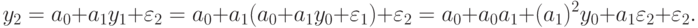
$y_{2} = a_{0} + a_{1}y_{1} +\varepsilon _{2} = a_{0} + a_{1}(a_{0} + a_{1}y_{0} + \varepsilon _{1}) + \varepsilon _{2} = a_{0} + a_{0}a_{1} + (a_{1})^{2}y_{0} + a_{1}\varepsilon _{2}+ \varepsilon _{2}.$

Продолжая процесс, найдем 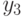$y_{3}$ :

$y_{3} = a_{0} + a_{1}y_{2} + \varepsilon _{3} = a_{0}[1 + a_{1} + (a_{1})^{2}] + (a_{1})^{3}y_{0} + (a_{1})^{2} \varepsilon _{1} + a_{1} \varepsilon _{2} + \varepsilon _{3}.$

Для итерации с номером получаем решение уравнения (9.7):

(9.8)

Предположим, что начальное значение 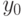$y_{0}$ неизвестно. Тогда при движении "назад" заменим 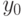$y_{0}$ на итерацию "назад" 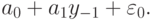$a_{0} + a_{1}y_{-1} + \varepsilon _{0}.$ В результате получаем:

Предполагая, что 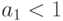$a_{1} < 1$ и сдвигаясь назад на m периодов 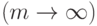$(m \to \infty )$ , получаем: Можно показать, что полученное решение уравнения (9.7) не единственное. Решением уравнения (9.7) при любом будет и выражение

(9.9)

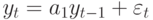Выражение (9.9), как и в случае дифференциальных уравнений первого порядка, представляет сумму общего решения $y_{t}^{одн} = Ca_{1}^{T }$ однородного разностного уравнения вида (9.2) $y_{t} = a_{1}y_{t-1} + \varepsilon _{t}$ и частного решения неоднородного уравнения (9.7).

Теперь рассмотрим случай 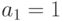$a_{1} = 1$ . Тогда движением "назад" получаем решение в виде 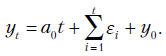В отличие от предыдущего случая здесь ошибки 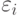$\varepsilon _{i}$ не убывают, а накапливаются.

Рассмотрим теперь уравнение второго порядка

$y_{t} - a_{1}y_{t-1} - a_{2}y_{t-2} = 0.$

(9.10)

Будем искать решение уравнения второго порядка в том же виде

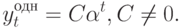
$y_{t}^{одн} = C\alpha ^{t}, C \ne 0.$

Подставляя это выражение в (9.10), получаем

$Сa_{t} - a_{1}Сa^{t-1} - a2Сa^{t-2} = 0.$

(9.11)

Разделив обе части (9.11) на $Сa^{t-2}$ , получим характеристическое уравнение $\alpha ^{2} - a_{1}\alpha - a_{2} = 0$ . При решении характеристического уравнения могут возникнуть три случая.

Случай 1. Дискриминант 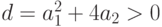$d = a_{1}^{2} + 4a_{2} > 0$ и существуют два действительных различных корня уравнения. Тогда

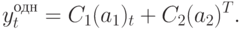
$y_{t}^{одн} = C_{1}(a_{1})_{t} + C_{2}(a_{2})^{T} .$

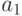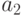Если абсолютное значение хотя бы одного из корней $a_{1}$ или $a_{2}$ превышает единицу, то однородное решение имеет "взрывной" характер при $t \to \infty$ .

Случай 2. Если 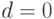d = 0 , то общее решение имеет вид

Решение носит "взрывной" характер при $|a_{1}| > 2$ . Если $|a_{1}| < 2$ , то из-за слагаемого поведение общего решения не так ясно. В итоге решение стремится к нулю, но вначале может носить "взрывной" характер.

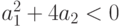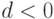Случай 3. Если $a_{1}^{2} + 4a_{2} < 0$ , то d < 0 и характеристические корни комплексные. В этом случае однородное решение может быть получено в виде 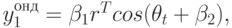$y_{1}^{онд }= \beta _{1}r^{T} cos(\theta_{t} +\beta _{2}),$ где $\beta _{1}, \beta _{2}$ - произвольные постоянные, а \theta удовлетворяет соотношению 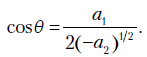Тригонометрическая функция создает волнообразное поведение решения однородного уравнения. 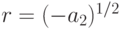Частота колебаний определяется параметром $\theta$ , а амплитуда колебаний - множителем $r = (-a_{2})^{1/2}$ . 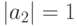Если $|a_{2}| = 1$ , то амплитуда не меняется. Колебания затухают при $|a_{2}| < 1$ и растут при $|a_{2}| > 1$ .

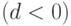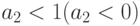Характеризация условий устойчивости. В случае существования двух корней характеристического уравнения для устойчивости требуется, чтобы оба корня находились внутри промежутка (-1; 1). В случае совпадающих характеристических корней условие устойчивости принимает вид $|a_{1}| < 2$ . Для комплексных корней в случае 3 (d < 0) условие устойчивости следующее: - $a_{2} < 1 (a_{2} < 0)$ .

Дальше >>

Введение в эконометрику

Введение в эконометрику

Разностные уравнения и их решение

9.1. Уравнения первого и второго порядков

Вопросы и ответы

Студенты

Авторизоваться

Введение в эконометрику

Введение в эконометрику

Разностные уравнения и их решение

9.1. Уравнения первого и второго порядков

Вопросы и ответы

Студенты