Нечеткие и гибридные нейронные сети

Интеллектуальные информационные системы в условиях неопределенности и риска

С помощью символьной обработки информации не удается решить прикладные задачи многих предметных областей, если для них невозможно получить полную информацию и если их определение недостаточно полно. Такая ситуация характерна для:

• сложных технических систем;
• систем экономического планирования;
• социальных систем большой размерности;
• систем принятия решений и т.п.

Выходом является использование систем, основанных на мягких вычислениях, которые включают в себя:

• нечеткую логику и вероятностные вычисления;
• нейрокомпьютинг - обучение, адаптация, классификация, системное моделирование и идентификация;
• генетические вычисления - синтез, настройка и оптимизация с помощью систематизированного случайного поиска и эволюции.

Эти составные части не конкурируют друг с другом, а создают эффект взаимного усиления (гибридные системы). Наряду с термином "мягкие вычисления" используется термин "вычислительный интеллект" - научное направление, где решаются задачи искусственного интеллекта на основе теории нечетких систем, нейронных сетей и эволюционных (генетических) вычислений.

Нечеткие нейронные сети с генетической настройкой параметров (гибридные системы) демонстрируют взаимное усиление достоинств и нивелирование недостатков отдельных методов:

1. Представление знаний в нейронных сетях в виде матриц весов не позволяет объяснить результаты проведенного распознавания или прогнозирования, тогда как в системах вывода на базе нечетких правил результаты воспринимаются как ответы на вопросы "почему?".
2. Нейронные сети обучаются с помощью универсального алгоритма, т.е. трудоемкое извлечение знаний заменяется сбором достаточной по объему обучающей выборки. Для нечетких систем вывода извлечение знаний включает в себя сложные процессы формализации понятий, определение функций принадлежности, формирование правил вывода.
3. Нечеткие нейронные сети обучаются как нейронные сети, но их результаты объясняются как в системах нечеткого вывода.

Нечеткие множества

Понятие нечетких множеств (fuzzy sets) как обобщение обычных (четких) множеств было введено Л.Заде в 1965 г.. Традиционный способ представления элемента множества состоит в применении характеристической функции , которая равна 1, если элемент принадлежит множеству , или равна 0 в противном случае. В нечетких системах элемент может частично принадлежать любому множеству. 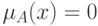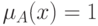Степень принадлежности множеству , представляющая собой обобщение характеристической функции, называется функцией принадлежности , причем , и означает отсутствие принадлежности множеству , а - полную принадлежность. Конкретное значение функции принадлежности называется степенью или коэффициентом принадлежности.