| Россия, Москва |
Задача нелинейного разделения двух классов
Метод максимума правдоподобия
Рассмотрим задачу разделения двух классов, с каждым из которых связано
вероятностное
распределение в пространстве векторов  значений признаков. Будем
обозначать
плотности этих распределений
значений признаков. Будем
обозначать
плотности этих распределений  - событие,
состоящее в том, что
объект принадлежит {
- событие,
состоящее в том, что
объект принадлежит {  }-му классу. Нас интересует апостериорная
вероятность:
}-му классу. Нас интересует апостериорная
вероятность:  — вероятность принадлежности объекта к
{
— вероятность принадлежности объекта к
{  }-му классу при условии, что
он характеризуется вектором признаков
}-му классу при условии, что
он характеризуется вектором признаков  Известная из теории
вероятности
формула Байеса
дает
Известная из теории
вероятности
формула Байеса
дает
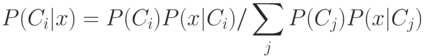
где 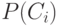 — вероятность появления объектов
{
— вероятность появления объектов
{  }-го класса. Для
нормальных
}-го класса. Для
нормальных  -мерных распределений
-мерных распределений
![P(x|Ci) = 1/ \{(2\pi )^{k/2}({det \sum}^i)^{1/2}exp [-\frac{1}{2}(x - M^i),
( {\sum}^i)^{-1}(x - M^i)]\},](/sites/default/files/tex_cache/4eb09fdbfe1036fb2fed0a95e4b08ebe.png)
где 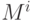 — математическое ожидание
— математическое ожидание  в
{
в
{  }-м классе,
{
}-м классе,
{ 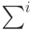 } — ковариационная матрица
для {
} — ковариационная матрица
для {  }-го класса. В результате обработки данных находят
статистические оценки {
}-го класса. В результате обработки данных находят
статистические оценки { 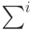 }
и
}
и 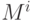 : пусть для {
: пусть для {  }-го класса имеются векторы
}-го класса имеются векторы 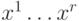 , тогда полагаем
, тогда полагаем
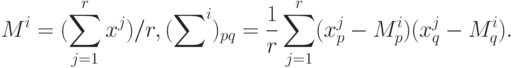
Минимизация в формуле Байеса дает простое решающее правило:  принадлежит
принадлежит  -му классу, если
-му классу, если  для всех
для всех 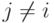 ,
т.е выбирается такой
класс, для которого вероятность
,
т.е выбирается такой
класс, для которого вероятность  максимальна. Поскольку в
формуле Байеса для всех
максимальна. Поскольку в
формуле Байеса для всех 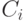 знаменатель общий, то решающее правило приобретает следующий вид:
выбираем то
знаменатель общий, то решающее правило приобретает следующий вид:
выбираем то  , для которого
, для которого  максимально. Для нормального распределения
удобно прологарифмировать эту величину. Окончательно получаем:
максимально. Для нормального распределения
удобно прологарифмировать эту величину. Окончательно получаем:
 принадлежит
принадлежит  -му классу, если среди величин
-му классу, если среди величин
![P_j = ln P(C_j) - (ln det {\sum}^j)/2 - [({x - M^j}), ({\sum}^j)^{-1}(x
- M^j)]/2](/sites/default/files/tex_cache/24b52b7d9d1827de1260c70af4fe1b68.png)
величина  - максимальная. Таким образом, разделяющей является
поверхность второго порядка,
а операцию разделения на два класса выполняет квадратичный адаптивный
сумматор в комбинации
с пороговым нелинейным элементом. Пороговый элемент вычисляет ступенчатую
функцию
- максимальная. Таким образом, разделяющей является
поверхность второго порядка,
а операцию разделения на два класса выполняет квадратичный адаптивный
сумматор в комбинации
с пороговым нелинейным элементом. Пороговый элемент вычисляет ступенчатую
функцию  ,
в результате для первого класса получим ответ 1, для второго - 0.
,
в результате для первого класса получим ответ 1, для второго - 0.
Нейрофизиологическая аналогия
Идея использования НС с квадратичными сумматорами для улучшения
способности сети к обобщению
базируется на хорошо известном факте индукции в естественных НС, когда
возбуждение в одних
областях мозга влияет на возбуждение в других. Простейшей формализацией этого
является введение
коэффициента, пропорционального сигналу от  -го нейрона, в
величину веса
-го нейрона, в
величину веса  -го сигнала
-го сигнала  -го
нейрона. Снабдив такое произведение весом
-го
нейрона. Снабдив такое произведение весом 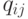 —
"коэффициентом индукции", получим
рассматриваемую архитектуру
—
"коэффициентом индукции", получим
рассматриваемую архитектуру
![y = f[Q(x) + L(x) + P],](/sites/default/files/tex_cache/a1721f501cee9d054c30fda9c4ef8615.png)
где 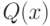 и
и 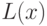 - соответственно квадратичная и
линейная функция,
- соответственно квадратичная и
линейная функция, 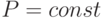 ,
,  - функция
активации нейрона. Коэффициенты функций
- функция
активации нейрона. Коэффициенты функций 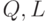 и константа
и константа  являются подстроечными
параметрами, определяющимися в ходе обучения.
являются подстроечными
параметрами, определяющимися в ходе обучения.
