Градиентные алгоритмы обучения сети

Универсальный путь обучения

Существует универсальный путь обучения нейронных сетей - минимизация оценки как неявно заданной функции параметров сети. При реализации этого подхода предполагается, что:

• задана обучающая выборка, состоящая из векторов входных сигналов ;
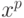• известны требования к соответствующим выходным сигналам , зафиксированные в функции оценки ;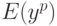
• оценка по всей выборке или какой-либо ее части строится известным способом по значениям .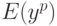

После подготовки (создание обучающей выборки, выбор функции оценки, предобработка входных данных и т.п.), предшествующей обучению, имеем способ вычисления некоторой функции , минимизация которой как функции параметров настроит сеть для правильной работы.

Особенности задачи оптимизации, возникающей при обучении нейронных сетей

Задачи оптимизации нейронных сетей имеют ряд специфических ограничений. Они связаны с огромной размерностью задачи обучения. Число параметров может достигать и более. В простейших программных имитаторах на персональных компьютерах подбирается - параметров. Из-за высокой размерности возникают два требования к алгоритму:

1. Ограничение по памяти. Пусть - число параметров. Если алгоритм требует затрат памяти порядка 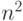, то он вряд ли применим для обучения. Желательно иметь алгоритмы, которые требуют затрат памяти .
2. Возможность параллельного вычисления наиболее трудоемких этапов алгоритма, и желательно нейронной сетью.
3. Обученный нейрокомпьютер должен с приемлемой точностью решать все тестовые задачи. Поэтому задача обучения становится многокритериальной задачей оптимизации: нужно найти точку общего минимума большого числа функций. Обучение нейрокомпьютера исходит из гипотезы о существовании этой точки.
4. Обученный нейрокомпьютер должен иметь возможность приобретать новые навыки без утраты старых. Возможно более слабое требование: новые навыки могут сопровождаться потерей точности в старых, но потеря не должна быть существенной. Это означает, что в достаточно большой окрестности найденной точки общего минимума оценок их значения незначительно отличаются от минимальных. Итак, имеем четыре специфических ограничения, выделяющих обучение нейрокомпьютера из общих задач оптимизации:

• астрономическое число параметров;
• необходимость высокого параллелизма при обучении;
• многокритериальность решаемых задач;
• необходимость найти достаточно широкую область, в которой значения всех минимизируемых функций близки к минимальным.