| Россия, Москва |
Градиентные алгоритмы обучения сети
Учет ограничений при обучении
Для параметров сети возможны ограничения простейшего вида:

Они вводятся из различных соображений: чтобы избежать слишком крутых или, наоборот, слишком пологих характеристик нейронов, чтобы предотвратить появления слишком больших коэффициентов усиления сигнала на синапсах и т.п.
Учесть ограничения можно, например, методом штрафных функций либо методом проекций:
- Использование метода штрафных функций означает, что в оценку
 добавляется штрафы за выход параметров из области ограничений. В~градиент
добавляется штрафы за выход параметров из области ограничений. В~градиент  вводятся производные штрафных функций.
вводятся производные штрафных функций. - Проективный метод означает, что если в сети предлагается изменение
параметров
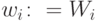 и
и  для некоторых
для некоторых  выходит за ограничения, то следует
положить
выходит за ограничения, то следует
положить
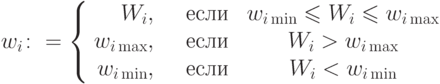
Практика показывает, что проективный метод не приводит к затруднениям. Обращение со штрафными функциями менее успешно. Далее будем считать, что ограничения учтены одним из методов, и будем говорить об обучении как о безусловной минимизации.
Выбор направления минимизации
Пусть задано начальное значение вектора параметров 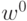 и
вычислена функция
оценки
и
вычислена функция
оценки  . Процедура одномерной оптимизации дает
приближенное
положение минимума
. Процедура одномерной оптимизации дает
приближенное
положение минимума  (вообще говоря, локального).
(вообще говоря, локального).
Наиболее очевидный выбор направления  для одномерной
оптимизации -
направление антиградиента
для одномерной
оптимизации -
направление антиградиента  :
:

Выберем на каждом шаге это направление, затем проведем одномерную
оптимизацию, потом снова вычислим градиент  и т.д. Это -
метод
наискорейшего спуска, который иногда работает хорошо. Но
неиспользование
информации о кривизне функции оценки (целевой функции) и резкое замедление
минимизации в окрестности точки оптимального решения, когда градиент
принимает очень малые значения, часто делают алгоритм наискорейшего спуска
низкоэффективным.
и т.д. Это -
метод
наискорейшего спуска, который иногда работает хорошо. Но
неиспользование
информации о кривизне функции оценки (целевой функции) и резкое замедление
минимизации в окрестности точки оптимального решения, когда градиент
принимает очень малые значения, часто делают алгоритм наискорейшего спуска
низкоэффективным.
Другой способ - случайный выбор направления  для одномерной
оптимизации.
Он требует большого числа шагов, но зато предельно прост — ему необходимо
только прямое функционирование сети с вычислением оценки.
для одномерной
оптимизации.
Он требует большого числа шагов, но зато предельно прост — ему необходимо
только прямое функционирование сети с вычислением оценки.

