| Россия, Москва |
Рекуррентные сети как ассоциативные запоминающие устройства
Введение
Отдельную группу нейронных сетей составляют сети с обратной связью между различными слоями нейронов. Это так называемые рекуррентные сети. Их общая черта состоит в передаче сигналов с выходного либо скрытого слоя на входной слой.
Благодаря обратной связи при подаче сигнала на входы сети, в ней возникает
переходный процесс, который завершается формированием нового устойчивого
состояния, отличающегося в общем случае от предыдущего. Если функцию
активации нейрона обозначить 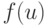 , где
, где  -
взвешенная сумма его
возбуждений, то состояние нейрона можно определить выходным сигналом
-
взвешенная сумма его
возбуждений, то состояние нейрона можно определить выходным сигналом  . Изменение состояния
. Изменение состояния  -го нейрона можно описать
системой дифференциальных уравнений
-го нейрона можно описать
системой дифференциальных уравнений

для 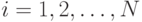 , где
, где 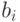 - пороговое значение.
- пороговое значение.
Рекуррентной сети можно поставить в соответствие энергетическую функцию Ляпунова
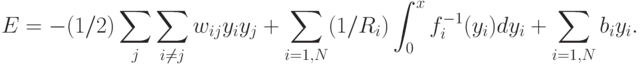
Изменение состояния какого-либо нейрона инициализирует изменение энергетического состояния сети в направлении минимума ее энергии вплоть до его достижения. В пространстве состояний локальные энергетические минимумы E представлены точками стабильности, называемыми аттракторами из-за тяготения к ним ближайшего окружения. Благодаря наличию аттракторов, рекуррентные сети могут быть использованы как устройства ассоциативной памяти.
Ассоциативная память играет роль системы, определяющей взаимную зависимость векторов. В случае, когда на взаимозависимость исследуются компоненты одного и того же вектора, говорят об автоассоциативной памяти. Если же взаимозависимыми оказываются два различных вектора, можно говорить о памяти гетероассоциативного типа. К первому классу относится сеть Хопфилда, а ко второму - сеть Хемминга и сеть типа BAM (Bidirectional Associative Memory - двунаправленная ассоциативная память).
Задача ассоциативной памяти сводится к запоминанию обучающих векторов, чтобы при представлении нового вектора система могла сгенерировать ответ - какой из запомненных ранее векторов наиболее близок к вновь поступившему образу. Часто в качестве меры близости отдельных множеств применяется расстояние Хемминга.
При использовании двоичных значений (0,1) расстояние Хемминга
между двумя
векторами 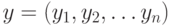 и
и 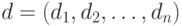 определяется в виде
определяется в виде
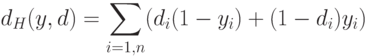
При биполярных значениях элементов обоих векторов расстояние Хемминга рассчитывается по формуле
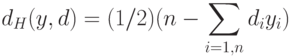
Мера Хемминга равна числу несовпадающих компонент двух векторов. Она равна
нулю, когда  .
.
