| Россия, Москва |
Нечеткие и гибридные нейронные сети
Лингвистические переменные
В теории нечетких множеств, помимо переменных цифрового типа, существуют лингвистические переменные с приписываемыми им значениями.
Пусть  обозначает температуру. Можно определить нечеткие
множества
"отрицательная", "близкая к нулю",
"положительная", характеризуемые
функциями принадлежности
обозначает температуру. Можно определить нечеткие
множества
"отрицательная", "близкая к нулю",
"положительная", характеризуемые
функциями принадлежности  ,
,  ,
,  . Лингвистическая
переменная "температура" может принимать значения
"отрицательная"
"близкая к нулю", "положительная". Функция нечеткой
принадлежности
является непрерывным приближением пороговой функции точной принадлежности.
. Лингвистическая
переменная "температура" может принимать значения
"отрицательная"
"близкая к нулю", "положительная". Функция нечеткой
принадлежности
является непрерывным приближением пороговой функции точной принадлежности.
Нечеткие правила вывода
если  это
это  , то
, то  это
это 
называется нечеткой
импликацией 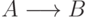 , если
, если  и
и  -
лингвистические значения
(значения лингвистической переменной), идентифицированные нечетким
способом через соответствующие функции принадлежности для переменных.
-
лингвистические значения
(значения лингвистической переменной), идентифицированные нечетким
способом через соответствующие функции принадлежности для переменных.
Часть "  это
это  " называется условием
(предпосылкой), а "
" называется условием
(предпосылкой), а "  это
это  " -
следствием (заключением).
" -
следствием (заключением).
Обобщение для  -мерного вектора
-мерного вектора  :
:
если  это
это  и
и  это
это  и
и  и
и  это
это 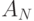 , то
, то  это
это  ,
, 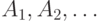 ,
, 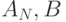 обозначают величины
соответствующих коэффициентов
принадлежности
обозначают величины
соответствующих коэффициентов
принадлежности 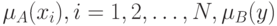 .
.
- в форме логического произведения
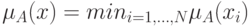
- в форме алгебраического произведения(агрегирование предпосылки).
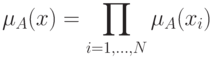
Каждой импликации 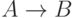 можно приписать значение функции
принадлежности
можно приписать значение функции
принадлежности 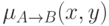 :
:
- форма логического произведения
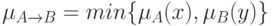
- форма алгебраического произведенияагрегирование на уровне импликации).