О деревьях
Каркасы в неориентированном графе
Число каркасов в неориентированном графе определяется с помощью следующей
матричной теоремы о деревьях в графе. Пусть  обозначает
матрицу, получаемую из матрицы
обозначает
матрицу, получаемую из матрицы 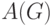 , где
, где 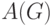 — матрица
смежности графа
— матрица
смежности графа  ,
с помощью подстановки в ней на место
,
с помощью подстановки в ней на место  -го диагонального элемента
числа
-го диагонального элемента
числа  .
.
Матричная теорема о деревьях для графов. Для
всякого связного помеченного графа  все алгебраические дополнения
матрицы
все алгебраические дополнения
матрицы  равны друг другу и их общее значение представляет собой число каркасов
графа
равны друг другу и их общее значение представляет собой число каркасов
графа  .
.
Пример. Для графа  (рис.11. 3) с матрицей смежности
(рис.11. 3) с матрицей смежности
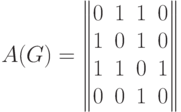
 имеет вид
имеет вид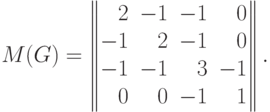
Алгебраическое дополнение, например, элемента  ,
равно
,
равно  .
Соответствующие каркасы графа
.
Соответствующие каркасы графа  показаны на (рис.11. 4).
показаны на (рис.11. 4).
Интересен также следующий результат. Пусть  -вершинный граф
без петель и
-вершинный граф
без петель и 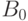 — его матрица инциденции с одной удаленной
строкой (т.е. с
— его матрица инциденции с одной удаленной
строкой (т.е. с 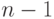 независимыми строками). Пусть
независимыми строками). Пусть 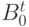 — транспонированная матрица к
— транспонированная матрица к 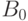 . Тогда определитель
. Тогда определитель 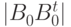 равен числу остовных деревьев графа
равен числу остовных деревьев графа  .
.
Каркасы в ориентированных графах
Число каркасов в ориентированном графе определяется с помощью аналогичной
матричной теоремы о деревьях в орграфе. Пусть  — орграф с
матрицей смежности
— орграф с
матрицей смежности 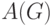 . Определим диагональную матрицу
. Определим диагональную матрицу 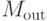 , у которой
, у которой 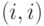 -й элемент равен полустепени исхода
-й элемент равен полустепени исхода  вершины
вершины 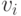 . Затем положим
. Затем положим  . Аналогично определяется матрица
. Аналогично определяется матрица 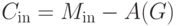 .
.
Матричная теорема о деревьях для орграфов. Все алгебраические дополнения  -й строки матрицы
-й строки матрицы 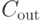 равны друг другу, и их общее значение есть число каркасов орграфа
равны друг другу, и их общее значение есть число каркасов орграфа  ,
входящих в вершину
,
входящих в вершину 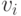 . Двойственным образом общее значение алгебраических
дополнений
. Двойственным образом общее значение алгебраических
дополнений  -го столбца матрицы
-го столбца матрицы 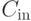 равно числу
каркасов, выходящих из вершины
равно числу
каркасов, выходящих из вершины 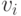 .
.
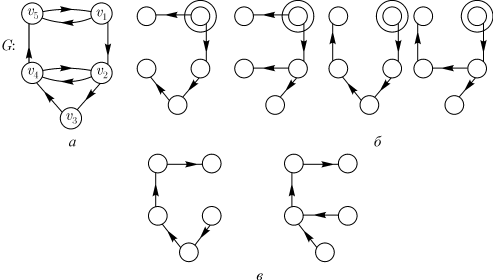
Пример. Для графа  (см. рис.11.5) матрицы
(см. рис.11.5) матрицы 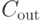 и
и 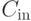 имеют вид:
имеют вид:
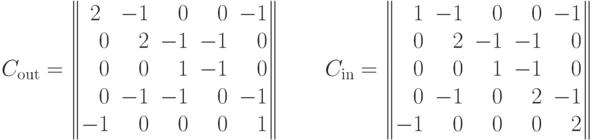
Используя их, убеждаемся сразу, исходя из первой строки матрицы 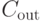 и из первого столбца матрицы
и из первого столбца матрицы 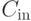 , что
орграф
, что
орграф  имеет
в точности четыре каркаса, выходящих из вершины
имеет
в точности четыре каркаса, выходящих из вершины  , и два каркаса,
входящих в эту вершину.
, и два каркаса,
входящих в эту вершину.