О деревьях
Перечисление и подсчет деревьев
Теорема (Кэли)
Число  помеченных деревьев с
помеченных деревьев с  вершинами равно
вершинами равно 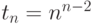 .
.
Теорема (Скойнса)
Число  -раскрашенных деревьев с
-раскрашенных деревьев с  вершинами одного
цвета и
вершинами одного
цвета и  вершинами другого равно
вершинами другого равно 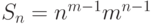 .
.
Теорема (Рида)
Число помеченных гомеоморфно несводимых деревьев равно 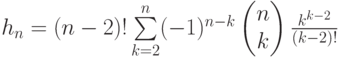 .
.
Непомеченные деревья
Пусть 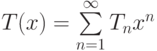 —
производящая функция
для корневых деревьев.
—
производящая функция
для корневых деревьев.
Таким образом, 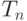 представляет собой
число корневых деревьев с
представляет собой
число корневых деревьев с  вершинами.
вершинами.
Теорема (Пойа) Перечисляющий ряд корневых деревьев удовлетворяет соотношению
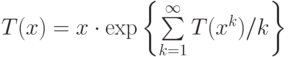 |
( *) |
Из этой теоремы следует, что 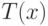 однозначно определяется
функциональным уравнением (*). Из данного уравнения выводится
формула для
однозначно определяется
функциональным уравнением (*). Из данного уравнения выводится
формула для 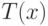 . Данную зависимость получил Кэли:
. Данную зависимость получил Кэли: 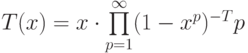 .
.
Следующая рекурсивная функция для вычисления 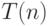 принадлежит
Оттеру.
принадлежит
Оттеру.
Пусть
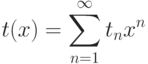
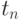 есть число деревьев с
есть число деревьев с  вершинами.
вершинами.Теорема (Оттера)
Ряд 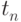 , перечисляющий деревья, выражается через ряд
, перечисляющий деревья, выражается через ряд 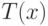 для корневых деревьев с помощью формулы
для корневых деревьев с помощью формулы 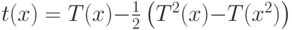 .
.
Ориентированные деревья
Пусть 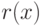 и
и 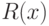 — перечисляющие ряды для
ориентированных и для
корневых ориентированных деревьев, соответственно.\medskip
— перечисляющие ряды для
ориентированных и для
корневых ориентированных деревьев, соответственно.\medskip
Теорема (Харари-Принса)
Перечисляющие ряды 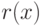 и
и 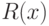 для ориентированных и
для корневых ориентированных деревьев удовлетворяют соотношениям
для ориентированных и
для корневых ориентированных деревьев удовлетворяют соотношениям 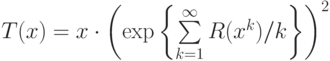 и
и 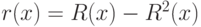 .
.
